Artigo 9: “Introducing exceptional growth mining— Analyzing the impact of soil characteristics on on-farm crop growth and yield variability”

A agricultura desempenha um papel fundamental na segurança alimentar e na economia global. Produzir alimentos de maneira eficiente é essencial para sustentar populações e garantir estabilidade econômica. No entanto, a variabilidade no crescimento das culturas e no rendimento das colheitas continua sendo um grande desafio. Essa variabilidade pode resultar em perdas econômicas significativas e insegurança alimentar. As características do solo, como a composição mineral, o pH e os níveis de nutrientes, desempenham um papel vital no crescimento das plantas. Compreender esses fatores é crucial para otimizar a produtividade agrícola, considerando também as condições climáticas e práticas de manejo.
É aqui que entra o artigo “Introducing Exceptional Growth Mining—Analyzing the Impact of Soil Characteristics on On-Farm Crop Growth and Yield Variability”. Os autores, Puck J. A. M. Mulders, Edwin R. van den Heuvel, Pytrik Reidsma e Wouter Duivesteijn, propõem uma abordagem inovadora chamada Exceptional Growth Mining (EGM) que explora a relação entre as características do solo e a produtividade das culturas. Esta técnica de mineração de dados visa identificar padrões de crescimento excepcionais das plantas, fornecendo aos agricultores insights valiosos para a tomada de decisões sobre o manejo do solo e das culturas.
Explorando Conceitos Chave
Descritores Utilizados
Foram utilizados diversos descritores relacionados às características do solo e aos parâmetros de crescimento das plantas. Entre os principais deles estão a concentração de nutrientes como nitrogênio (N), fósforo (P) e potássio (K), níveis de umidade do solo em diferentes estágios de crescimento e parâmetros de crescimento como a taxa de crescimento e tamanho das plantas.
Curvas de Crescimento
Modeladas utilizando modelos mistos não lineares, que incorporam efeitos fixos e aleatórios, para capturar tanto os padrões comuns quanto a variabilidade específica de subgrupos.
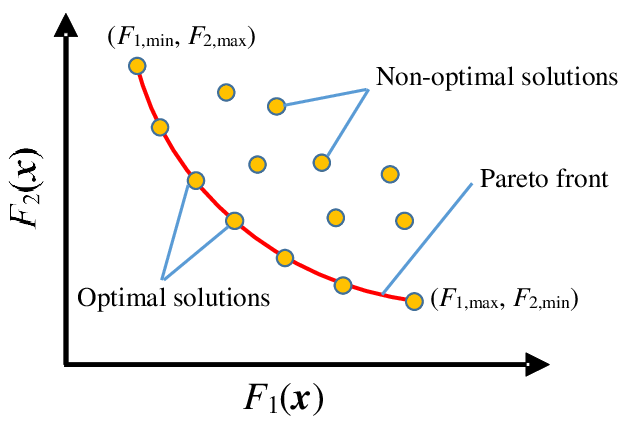
Fronteira de Pareto
Utilizada para filtrar subgrupos, garantindo que apenas os mais excepcionais sejam considerados. Ela consiste no conjunto de subgrupos que não são dominados por outros em todos os critérios avaliados.
Entendendo o Algoritmo EGM
O EGM é projetado para identificar subgrupos de dados com crescimento excepcional, destacando aqueles que se desviam significativamente dos padrões normais.
Dados Necessários
O algoritmo EGM requer dados longitudinais das plantações, o que significa que as informações devem ser coletadas ao longo do tempo, permitindo a análise do desenvolvimento das plantas em diferentes condições. As variáveis principais analisadas incluem nutrientes do solo, umidade e crescimento das plantas (medido em termos de altura), peso e produtividade ao longo do tempo.
Curvas de Crescimento
As curvas de crescimento são representações matemáticas que descrevem como as plantas se desenvolvem ao longo do tempo. Elas são fundamentais para entender e prever o comportamento das plantas em diferentes condições ambientais e de manejo agrícola.
Para modelar essas curvas, o algoritmo utiliza modelos mistos não lineares que incluem:
- Componentes Fixos: Representam os efeitos comuns que afetam todas as observações de forma consistente, como a influência média dos nutrientes do solo em todas as plantas.
- Componentes Aleatórios: Capturam a variabilidade específica entre subgrupos, permitindo que o modelo se ajuste às diferenças individuais.
A qualidade do ajuste dessas curvas é avaliada pelo coeficiente de determinação \(R^2\), que indica quão bem o modelo explica a variação nos dados.
Mineração de Modelos Excepcionais (EMM)
A Mineração de Modelos Excepcionais (Exceptional Model Mining - EMM) é um framework de mineração de padrões locais, projetado para encontrar subgrupos interessantes em conjuntos de dados. Os subgrupos são considerados interessantes se forem interpretáveis e excepcionais.
No artigo, a fase final do EGM envolve a identificação de subgrupos que apresentam crescimento excepcional e métodos estatísticos são empregados para distinguir os subgrupos mais relevantes, assegurando que os padrões identificados não sejam devido ao acaso, mas sim o reflexo de fenômenos importantes nos dados.
Metodologia Experimental
Coleta de Dados
Os dados foram coletados na fazenda de batatas Van den Borne Aardappelen, no sul da Holanda, entre 2015 e 2018. O dataset abrange informações sobre níveis de nutrientes (como nitrogênio, potássio, fósforo, entre outros) em cada campo de plantação, mas não inclui dados climáticos ou informações de pH do solo.
Para cada ano, cinco a sete amostragens foram feitas em aproximadamente 100 campos. Em cada amostragem, três plantas de batata foram selecionadas e os tubérculos foram pesados para calcular o peso por metro quadrado através da fórmula: \(y({gr}\times{m^{-2}}) = \frac{{\tilde{y}(\text {gr/3 plants})} \times 1.333}{\text {planting distance (cm)}\times {\frac{3}{100}}}\)
Além disso, a coleta das batatas foi realizada no ponto médio de condutividade elétrica de cada campo, medida com o uso do dispositivo DUALEM-21s. Esse cuidado é importante porque campos com alta condutividade elétrica são ricos em sal, o que pode prejudicar o crescimento das plantações.
Modelagem de Curvas de Crescimento
Para a modelagem das curvas foi usado o peso dos tubérculos ao longo do tempo e um coeficiente de erro para balancear a função de crescimento, já que não haviam dados climáticos. Para estimar os pontos da curva de crescimento, foram utilizadas três variáveis principais:
- Crescimento máximo: Representa o valor máximo atingido pela curva de crescimento
- \(a_{ik} = \alpha_{0k} + \sigma_{\alpha}a_i\)
- Inclinação: Indica a rapidez com que o crescimento ocorre
- \(b_{ik} = \exp\{\beta_{0k} + \sigma_{\beta}b_i\}\)
- Ponto médio de crescimento: Ponto onde ocorre o crescimento mais rápido
- \(c_{ik} = \gamma_{0k} + \exp\{\sigma_{\gamma}\}c_i\)
A correlação entre essas variáveis foi explorada com o método “NLMIXED” disponível no software SAS. O resultado foi uma correlação bastante negativa entre o crescimento máximo e a inclinação, sugerindo que curvas de crescimento mais íngremes tendem a resultar em batatas com pesos menores.
De forma similar, foi também identificada uma correlação negativa entre a inclinação da curva e o ponto médio de crescimento, o que indica que curvas mais íngremes tendem a alcançar o ponto médio de crescimento mais cedo.
Ao fim, a equação da curva de crescimento é:
\(y^{TW}_{ijk} = \frac{\exp(a_{ik})}{1 + \exp\{-b_{ik} \cdot \exp(t_{ijk} - c_{ijk})\}} \exp(e_{ijk})\)
Para determinar a qualidade das curvas foi utilizada a métrica \(R^2\), que mede o quanto as variáveis dependentes são explicadas pelas variáveis independentes. O resultado foi \(R^2=0.92\), indicando uma boa adequação do modelo aos dados.
Aplicação do Exceptional Growth Mining (EGM)
A Mineração de Crescimentos Excepcionais (EGM) foi feita com o algoritmo Beam Search, com valor de profundidade (\(d\)) definido como 2 ou 3, o que garantiu que todos os subgrupos tivessem ao menos 15 itens.
Com a identificação dos subgrupos iniciais, foi aplicado um pós-processamento que selecionava os subgrupos mais relevantes com análise por Fronteira de Pareto. A fronteira de Pareto é responsável por encontrar o elemento dito Pareto eficiente, que não é capaz de ser melhorado em uma das métricas de avaliação sem piorar pelo menos alguma outra.
Ao fim, foram selecionados os cinco principais subgrupos para exibição na seção de resultados.
Análise Crítica dos Resultados
Além da análise de correlação entre as variáveis, como foi mostrado na seção anterior, também ocorreu a análise das variáveis em relação aos dados disponíveis das plantações, buscando identificar quais parâmetros eram mais influentes nos parâmetros das curvas. A seguir estão listados cada uma das informações disponíveis, em conjunto com a relação notada com as variáveis da curva de crescimento.
Nitrogênio: Influente na inclinação da curva de crescimento, sendo que maior teor de nitrogênio no solo levava a inclinações mais acentuadas e menores pesos máximos das batatas.
Potássio: Maiores níveis de potássio no solo estão diretamente associados a maior crescimento das batatas, sendo que baixos níveis desse elemento no solo resultam em batatas menores. Isso indica que a riqueza do solo em potássio é essencial para o sucesso da plantação.
Cálcio e Zinco: A combinação de altos níveis de Cálcio com baixos níveis de Zinco resultou em maior crescimento máximo das batatas.
Magnésio: Níveis elevados de magnésio no solo aceleram o crescimento, denotado pela maior inclinação da curva, enquanto níveis mais baixos desaceleram. O Magnésio é um elemento ideal para a síntese de clorofila e qualidade da batata, tendo também forte correlação positiva com o ponto médio de crescimento e crescimento máximo das batatas.
Ferro: O Ferro é essencial para várias funções celulares, mas a presença em demasia no solo pode ser tóxica para as plantas. Foi observado que tanto níveis muito altos quanto níveis muito baixos do elemento no solo prejudicam o crescimento.
Manganês e Zinco: Quando ocorrem níveis elevados de qualquer um dos dois elementos, o rendimento total das batatas fica prejudicado. Foi constatada uma correlação complexa entre o ph do solo e a presença desses dois minerais
Impactos Sociais do Exceptional Growth Mining (EGM)
A Mineração de Crescimento Excepcional (EGM) é uma ferramenta poderosa para identificar padrões de crescimento, podendo ser aplicada em diversos setores que vão muito além da agricultura, como mostrado no artigo. As seções a seguir são destinadas a explorar possibilidades de utilização desta técnica com perspectivas positivos e negativos.
Perspectiva Positiva
Além da utilização da agricultura para otimizar técnicas de plantio, como destacado no artigo, é possível citar:
Segurança alimentar: Em países com conflitos, desastres naturais, terras menos férteis, entre outros problemas, é possível utilizar a técnica do EGM para identificar áreas de solo mais produtivas e otimizar o uso de recursos limitados, o que contribui para maior segurança alimentar e sustentabilidade. Na mesma linha de pensamento, a técnica pode ser empregada para otimizar a criação de animais para consumo humano.
Redução de produtos tóxicos nas plantações: A aplicação de EGM nas plantações pode ocorrer também para reduzir o uso excessivo de fertilizantes e outros insumos agrícolas, identificando as necessidades de nutrientes do solo com maior exatidão. Isso não só melhora a qualidade dos alimentos produzidos para consumo humano e minimiza o impacto ambiental dos produtos industrializados, mas também reduz os custos dos produtores.
Medicina personalizada: A técnica de EGM pode ser aplicada na área da saúde para identificar crescimentos excepcionais de tumores, populações de vírus, bactérias ou fungos quando expostos a diferentes medicamentos, em diferentes pacientes.
Perspectiva Negativa
Apesar dos pontos positivos citados, o uso indiscriminado da técnica pode acarretar em problemas, como:
Desigualdade competitiva: Enquanto grandes produtores agrícolas e pecuários tendem a ter mais recursos para investir em otimizações, outros produtores podem não ter condições para acompanhar o progresso, levando a um agravamento da deslealdade de competição.
Otimização de armamentos biológicos: Enquanto a aplicação da técnica de EGM pode trazer grandes benefícios para tratamentos médicos personalizados, assim como foi dito anteriormente, o mesmo princípio pode ser aplicado para identificar carecterísticas necessárias para que populações de microorganismos prejudiciais à saúde humana cresçam em um hospedeito.
Conclusão
O Exceptional Growth Mining (EGM) é uma técnica de análise de dados que identifica subgrupos excepcionais em conjuntos de dados agrícolas. O EGM não estabelece causalidade, mas revela correlações significativas que podem orientar pesquisas futuras e otimizar práticas no setor. A robustez do método se deve ao uso de modelos mistos não lineares, permitindo a análise de dados ausentes e irregularmente espaçados - uma característica comum em estudos agrícolas.
Contudo, a aplicação do EGM suscita questões éticas, principalmente relacionadas à desigualdade, privacidade e segurança de dados. Estas preocupações não devem ser subestimadas e requerem atenção cuidadosa dos pesquisadores e profissionais que utilizam a técnica. A utilização responsável do EGM pode contribuir significativamente para o avanço da pesquisa agrícola e o desenvolvimento de práticas mais sustentáveis no setor.
Referências
Mulders, P. J. A. M., van den Heuvel, E. R., Reidsma, P., & Duivesteijn, W. (2024). Introducing exceptional growth mining—Analyzing the impact of soil characteristics on on-farm crop growth and yield variability. PLOS ONE, 19(1), e0296684. https://doi.org/10.1371/journal.pone.0296684
Apêndice
Acesso ao Dataset e Código Fonte
O código para o método de Mineração de Crescimento Excepcional (Exceptional Growth Mining - EGM) foi disponibilizado pelos autores deste artigo. O acesso ao código e aos dados pode ser realizado através do seguinte link: Exceptional Growth Mining data. Para obter os dados brutos, entre em contato com Jacob van den Borne pelo e-mail jacob@vandenborneaardappelen.com.
Mineração de Padrões Excepcionais: EMM.py
A função EMM é um método que realiza mineração de padrões excepcionais. O objetivo é encontrar descrições que maximizem uma medida de qualidade em um conjunto de dados. A função opera de acordo com os seguintes parâmetros:
w: Largura do feixe.d: Número de níveis.q: Número máximo de resultados.eta: Uma função que recebe uma descrição e retorna todos os refinamentos possíveis.satisfies_all: Uma função que verifica se uma descrição atende a determinados requisitos.eval_quality: Retorna a qualidade de uma descrição, que deve ser comparável às qualidades de outras descrições.catch_all_description: A descrição que equivale a “verdadeiro” ou “todos”, de modo que todo o conjunto de dados corresponda.
No final, é retornado conjunto de resultados (resultSet) com as melhores descrições encontradas.
Exemplo de chamada: EMM(w=10, d=5, q=50, eta=func_eta, satisfies_all=func_satisfies_all, eval_quality=func_eval_quality, catch_all_description=True)
Gerando Curvas de Crescimento: growth_curve.sas
Este script SAS é utilizado para calcular os parâmetros da curva de crescimento das batatas. Ele começa preparando os dados, ordenando-os por ano e calculando a média dos dias até o plantio. Em seguida, categoriza o tempo de plantio como “early” (cedo), “average” (médio) ou “late” (tardio) com base na média. Posteriormente, ele transforma e filtra os dados para garantir que apenas observações válidas e relevantes sejam utilizadas no ajuste das curvas de crescimento.
Na prática, o script usa o procedimento proc nlmixed para ajustar um modelo de mistura não linear aos dados, estimando parâmetros específicos para cada ano e variáveis aleatórias para cada campo de batata. Ele especifica os parâmetros iniciais, os limites de variabilidade e as correlações entre as variáveis aleatórias. O resultado final inclui as previsões dos parâmetros ajustados e a curva de crescimento ajustada, permitindo ao leitor entender e prever o crescimento das batatas ao longo dos anos com base nos dados fornecidos.
Análise de Subgrupos: pareto_front.ipynb
O Jupyter Notebook contém 6 arquivos, cada um correspondendo a um conceito-alvo, como variação dos parâmetros da curva (high/low e a/b/c). Dado que pode haver uma quantidade exorbitante de subgrupos excepcionais, este código é responsável por identificar os subgrupos que pertencem ao ótimo de Pareto para cada conceito-alvo. O código recebe como entrada o DataFrame resultante do EMM, produzindo uma saída semelhante, porém com um número reduzido de subgrupos.
Ele começa lendo os dados de um arquivo CSV e visualizando a relação entre a média (Mean) e o desvio padrão (Std) com um gráfico de dispersão. Em seguida, define a função identify_pareto, que compara cada ponto do conjunto de dados para verificar se ele é dominado por outros, determinando assim se pertence ao ótimo de Pareto. O código usa as médias absolutas, o inverso do desvio padrão e o número de subgrupos (n) para criar um conjunto de pontuações. A função retorna os índices dos pontos no ótimo de Pareto, que são extraídos e ordenados, filtrando o DataFrame para destacar os subgrupos mais relevantes.
Formato do Dataset
| Feature(s) | Descrição | Unidade | Observação |
|---|---|---|---|
| Nutrient_content | Classificação estimada pelo agricultor | - | - |
| Previously_cultivated_crop | Nome da cultura anterior | - | Cultivada por Van den Borne ou outro agricultor |
| Dryness | Umidade relativa | % | - |
| Nematodes | Presença de nematoides | yes/no | Praga que afeta batatas |
| N_soil, S_soil, K_soil, Mg_soil, Si_soil | Conteúdo de nutrientes do solo | kg/ha | Coletado desde 2015 |
| Fe_soil, Zn_soil, Ca_soil, Mn_soil, B_soil, P_soil | Conteúdo de minerais do solo | g/ha ou kg/ha | Coletado no mesmo local das amostras |
Formato de Saída
| Quality | Description | Mean | Std | t | n |
|---|---|---|---|---|---|
| Qualidade do resultado | Agrupamento de descritores do resultado | Média | Desvio Padrão | Valor t | Número de campos de batata pertencentes ao subgrupo |