Artigo 6: Discovering a Taste for the Unusual: Exceptionla Models for Preference Mining

Mineração de modelos excepcionais (Exceptional Model Mining - EMM) é um framework que tem como objetivo encontrar padrões locais, assim como a descoberta de subgrupos (Sbugroup Discovery - SD), porém EMM busca encontrar correlações entre variáveis alvo que podem ser consideradas interessantes/exepcionais. Já SD busca encontrar padrões, criando seletores nos atributos disponíveis, para encontrar individuos que atendam um padrão de qualidade em relação a distribuição de uma única variável alvo.

O artigo aborda uma técnica chamada mineração de preferências exepcionais (Excepional Preference Mining - EPM), onde procura-se achar preferência sobre rótulos, ou seja, encontrar preferências excepcionais de diversas opções possíveis sobre uma variável.

Contextualização do problema

Diversas linhas de pesquisa buscam construir modelos preditivos capazes de realizarem um ajuste global a um conjunto de dados, de forma fornecer resultados generalizados para todo o conjunto de dados que foi treinado, além de prever com acurácia novos conjuntos de dados. Esses modelos podem fornecer grande ajuda em tomadas de decisão, pois são capazes de preverem uma variável alvo. Contudo, pode-se extrair informações valiosas procurando padrões locais. Em casos como: eleições, market-places, restaurantes, sistemas de recomendação em redes sociais. O objetivo é tentar encontrar padrões de preferência, onde seria possível encontrar atributos de amostras que caracterizam essas preferências.

Busca-se portanto encontrar correlações entre os rótulos, objetivando encontrar uma preferência entre eles em grupos locais, considerados excepcionais.

Descoberta de Modelos Excepcionais - Imagem Gerada por DALL-E

Entre os métodos que realizam funções semelhantes a EPM, pode-se destacar o uso de regras de associação, proposto por Henzgen e Hullermeier, que faz uma busca por padrões de subranking.

Conceitos importantes

Label Ranking

Dada uma instância a \(x = \{a_1, a_2, \ldots, a_m, \pi\}\) do espaço de instâncias \(\mathbb{X}\), o objetivo é prever o rank dos rótulos \(\mathbb{L} = \{\lambda_1, \ldots, \lambda_n\}\) associados com \(x\). O ranking pode ser representado como uma strict total order sob \(\mathbb{L}\), definido no espaço de permutação \(\Omega\).

O Label Ranking se assemelha às tarefas de classificação, mas ao invés de prever uma classe, deseja-se ranquear os rótulos. Na classificação, cada instância é associada a uma distribuição probabilística sob \(\Omega\). Isso significa que, para cada \(x \in \mathbb{X}\), existe uma distribuição de probabilidade \(\mathbb{P}(.|x)\), de forma que para cada \(\pi \in \Omega\), \(\mathbb{P}(\pi|x)\) é a probabilidade de que \(\pi\) está associado ao ranking de \(x\). O objetivo de Label Ranking é mapear \(\mathbb{X} \rightarrow \Omega\).

Descoberta de Subgrupos e Exceptional Model Mining

A linguagem usada para retornar um subgrupo é a seguinte:

\(𝐴𝑔𝑒 ≥ 30 ⋀ 𝐿𝑖𝑘𝑒𝑠 = 𝑆𝑎𝑙𝑚𝑜𝑛 𝑅𝑜𝑒 → 𝑈𝑛𝑢𝑠𝑢𝑎𝑙\)

Métrica de Qualidade

Na mineração de padrões, o quão interessante um padrão pode ser é medido pela sua frequência; já em Subgroup Discovery (SD) essa métrica é estimada de forma supervisionada. Dada uma variável alvo \(t_1\) identificada no dataset, o quão interessante um subgrupo nela for, é medido pelo quão não-usual a distribuição dele neste alvo.

Se em uma população o comum é as pessoas gostarem de sushi chutoro, um subgrupo interessante seria de pessoas que gostam de Makizushi:

\(Age ≥ 30 ⋀ Lives in Region = Hokkaido → Makizushi\)

Se ao invés de usar um único atributo alvo, múltiplos alvos \(t_1, \ldots, t_l\) estão disponíveis, e se não estiver interessado em descobrir distribuições não usuais em um alvo, mas na interação entre alvos, pode-se então empregar o Exceptional Model Mining (EMM) no lugar do SD. Essa tarefa consiste em dois fatores: Model Class e Métrica de Qualidade.

Model Class é definido para representar uma interação não comum entre múltiplos alvos que se esteja interessado. Já a métrica de qualidade é usada para definir o que não é usual e, portanto, interessante.

Um exemplo seria tentar encontrar uma correlação entre a altura de uma pessoa \(( t_1 )\) e a altura média dos avós \(( t_2 )\). Para isso, é necessário achar um coeficiente de correlação entre $t_1 $ e \(t_2\). Nesse caso aplica-se EMM com um correlation model class. No caso de subgrupos muito pequenos, o modelo pode acabar favorecendo-os por serem pouco usuais. Para favorecer subgrupos maiores, deve-se definir uma métrica de qualidade que balanceie o quão excepcional um subgrupo é, e o tamanho dele.

Estratégia de Busca

Em EMM é explorado um amplo espaço de busca, guiado por uma métrica de qualidade para expressar a excepcionalidade buscada. Tipicamente, os subgrupos são buscados em uma busca por nível, combinando atributos da mesma forma que é feita uma combinação de itemsets para mineração de padrões frequentes.

A maioria dos algoritmos de busca, fazem de forma generalista-para-específico, tratando o espaço de busca como um lattice cuja estrutura é definida por um refinement operator \(\eta: \mathbb{D} \rightarrow 2^\mathbb{D}\). Esse operador consegue determinar como descrições podem ser estendidas para descrições mais complexas por adições atômicas. A aplicação proposta no artigo assume que \(\eta\) é um specialization operator: toda descrição $q $ é um elemento do conjunto \(\eta(p)\), o qual é mais especializada que a descrição \(p\) em si. O algoritmo, portanto, retorna uma lista ranqueada de descrições que satisfazem as especificações do usuário.

A estratégia de busca empregada foi um best first search, em cada nível as descrições são ordenadas pela métrica de qualidade \(\varphi\). O limite superior é o grau de complexidade, geralmente limitado por especialistas, para obter descrições com quantidades ideais de atributos para interpretação (profundidade da busca); e o limite inferior é o suporte dos subgrupos.

Regras de Distribuições

Regras de Distribuições (Distribution Rules, DR) é um método de SD para analisar uma única variável alvo. Ao invés de valores representativos (média, desvio-padrão etc.), DR identifica distribuições usuais do alvo, encontrando subgrupos expressados pelas regras de associação com a distribuição consequente:

\(S → t = Dist_t|S\)

• \(S\): é um conjunto de condições correspondentes à parte antecedente do DR (um subgrupo).
• \(t\): é a propriedade de interesse (ou o alvo).
• \(Dist_t|S\): é uma distribuição empírica de \(t\) quando \(S\) é observado. Ela é representada por um conjunto de pares $t_i, freq(t_i) $, onde \(t_i\) é um valor particular de \(t\) encontrado quando \(S\) é observado; \(freq(t_i)\) é a frequência de \(t_i\) quando os itens de \(S\) são observados.

Matriz de Preferência

Em EMP o conceito alvo consiste em um único alvo, o que faz sentido em SD. Contudo, o objeto alvo é um ranqueamento de rótulos, que pode ser representando como comparações em pares. Portanto, representa interações entre múltiplos rótulos individuais, o que é mais consistente no cenário do EMM.

Ranqueamento de rótulos pode ser difícil de analisar e visualizar, quando há uma quantidade grande de rótulos. O apresentado Sushi dataset, que contém 5000 amostras de opiniões de pessoas e 10 tipos de sushi mostra um exemplo real. Até essa quantidade modesta de tipos de sushi diferentes pode ser ranqueado em diversas combinações. Isso pode ter um impacto significativo, onde mais de 98% dos 5000 rankings presentes no dataset são únicos.

Por conta disso, os autores apresentaram uma alternativa para ranquear os rótulos, introduzindo as Matrizes de Preferência. A matriz de preferência (PM, preference matrix) é uma representação alternativa dos rankings em um conjunto de dados que facilita a análise de comportamentos de preferência excepcionais. Em vez de representar diretamente a ordenação dos rótulos, a matriz de preferência captura as comparações par a par entre rótulos, permitindo uma visão mais detalhada das relações de preferência.

Representar um conjunto de rankings por PM tem certas vantagens sob as tradicionais representações por permutações. PM podem, naturalmente, derivar uma variedade de conjunto métricas para busca de padrões de preferência. Contudo, há certas limitações também, a escolha de agregação de métricas pode esconder informações relevantes nas PMs, por exemplo, escolhendo a média se metade dos rankings minerados forem opostos, o resultando em entradas na PM são iguais a zero. Por isso subgrupos com PM contendo apenas zeros nas entradas são ignorados.

Entendendo os algoritmos usados

O algoritmo EPM (Exceptional Preference Mining) tem como objetivo identificar subgrupos significativos em um dataset, utilizando uma medida de qualidade para avaliar a diferença entre as preferências do subgrupo e do dataset original.

function EPM(dataset, quality_measure):
    dataset_pm = compute_preference_matrix(dataset)
    candidate_subgroups = generate_candidate_subgroups(dataset)

    for subgroup in candidate_subgroups:
        subgroup_pm = compute_preference_matrix(subgroup)
        distance = calculate_distance(dataset_pm, subgroup_pm, quality_measure)
        subgroup.score = calculate_score(distance, subgroup.size)

    ranked_subgroups = rank_subgroups(dataset_pm, candidate_subgroups)
    significant_subgroups = validate_subgroups(ranked_subgroups)

    return significant_subgroups

Passo a Passo do Algoritmo

Vamos apresentar o algoritmo EPM (Exceptional Preference Mining): 1. Função Principal

   function EPM(dataset, quality_measure):

A função principal EPM recebe dois parâmetros:

dataset: o conjunto de dados a ser analisado.
quality_measure: a medida de qualidade utilizada para avaliar as preferências.

2. Computação da Matriz de Preferência do Dataset

dataset_pm = compute_preference_matrix(dataset)

compute_preference_matrix(dataset): Calcula a matriz de preferência para o dataset completo, que será utilizada como referência para comparar os subgrupos.

1. Geração de Subgrupos Candidatos

candidate_subgroups = generate_candidate_subgroups(dataset)

generate_candidate_subgroups(dataset): Gera uma lista de subgrupos candidatos a partir do dataset original. Esses subgrupos serão avaliados posteriormente.

1. Avaliação dos Subgrupos Candidatos Para cada subgrupo na lista de candidatos, realiza-se os seguintes passos:

for subgroup in candidate_subgroups:
    subgroup_pm = compute_preference_matrix(subgroup)
    distance = calculate_distance(dataset_pm, subgroup_pm, quality_measure)
    subgroup.score = calculate_score(distance, subgroup.size)

compute_preference_matrix(subgroup): Calcula a matriz de preferência para o subgrupo específico.
calculate_distance(dataset_pm, subgroup_pm, quality_measure): Calcula a distância entre a matriz de preferência do dataset completo e a do subgrupo, utilizando a medida de qualidade fornecida.

Fórmula Geral

A distância geral \(L_S\) entre a matriz de preferência do dataset completo \(M_D\) e a matriz de preferência do subgrupo \(M_S\) é calculada como:

\(L_S = \frac{1}{2} (M_D - M_S)\)

Medidas de Qualidade

Norm

A medida de qualidade Norm é definida como a norma de Frobenius da matriz \(L_S\). A fórmula é:

\(\text{Norm}(S) = \| L_S \|_F = \sqrt{s/n} \cdot \sqrt{ \sum_{i=1}^{k} \sum_{j=1}^{k} L(i,j)^2 }\)

Labelwise

A medida de qualidade Labelwise é calculada como o valor máximo entre todas as somas das linhas da matriz \(L_S\):

\(\text{Labelwise}(S) = \max_{i=1,\ldots,k} \frac{1}{k(k-1)} \sum_{j=1}^{k} L(i,j)\)

Pairwise

A medida de qualidade Pairwise é calculada como o valor máximo entre todos os elementos da matriz \(L_S\):

\(\text{Pairwise}(S) = \max_{i,j=1,\ldots,k} L(i,j)\)

Essas medidas são utilizadas para avaliar a diferença entre as preferências do dataset original e dos subgrupos, ajudando a identificar subgrupos excepcionais.

calculate_score(distance, subgroup.size): Calcula a pontuação do subgrupo com base na distância calculada e no tamanho do subgrupo.

Passos para Calcular a Pontuação

Calcular a Cobertura Normalizada do Grupo

A Cobertura Normalizada do Grupo é dada por:

\(\sqrt{\frac{s}{n}}\)

onde: - \(s\) é o tamanho do subgrupo. - \(n\) é o tamanho do dataset completo.

Multiplicar pela Distância

A pontuação final do subgrupo é obtida multiplicando a Cobertura Normalizada do Grupo pela Distância calculada na função calculate_distance.

1. Ranqueamento dos Subgrupos

ranked_subgroups = rank_subgroups(dataset_pm, candidate_subgroups)

rank_subgroups(dataset_pm, candidate_subgroups): Ordena os subgrupos candidatos com base na pontuação calculada, gerando uma lista de subgrupos ranqueados.

Fórmula da Covariância Ponderada

A fórmula utilizada para calcular a covariância ponderada entre o vetor da matriz de preferência do dataset completo \(\text{vec}(M_D)\) e o vetor da matriz de preferência do subgrupo \(\text{vec}(M_S)\) é:

\(\text{RWCov}(S) = -\sqrt{\frac{s}{n}} \cdot \text{cov}(\text{vec}(M_D), \text{vec}(M_S))\)

onde:
- \(\text{vec}(M_D)\) é o vetor da matriz de preferência do dataset completo.
- \(\text{vec}(M_S)\) é o vetor da matriz de preferência do subgrupo.
- \(\text{cov}\) representa a covariância entre os dois vetores.
- \(s\) é o tamanho do subgrupo.
- \(n\) é o tamanho do dataset completo.

Esta medida ajuda a identificar subgrupos que possuem preferências excepcionalmente diferentes em relação ao dataset original.

1. Validação dos Subgrupos Significativos

significant_subgroups = validate_subgroups(ranked_subgroups)

validate_subgroups(ranked_subgroups): Valida os subgrupos ranqueados para identificar aqueles que são estatisticamente significativos.

1. Retorno dos Subgrupos Significativos Retorno dos Subgrupos Significativos

return significant_subgroups

Metodologia

Para fazer os experimentos, os autores incorporaram EPM no Cortana, que oferece uma estrutura genérica para descoberta de subgrupos e possui ferramentas para que diferentes abordagens de SD sejam aplicadas. Além disso, eles definiram uma linguagem de descrição para os subgrupos, que é composta por conjunções lógicas de restrições para atributos individuais.

A estratégia adotada para percorrer o espaço de busca foi uma best-first search gulosa. Sendo que os atributos numéricos foram discretizados com on fly greedy best-first search contendo 8 bins de mesma largura. Os resultados encontrados passaram pela validação DFD, que serve para evitar que subgrupos sejam selecionados por fatores aleatórios. A validação DFD consiste na criação de cópias do dataset, com algumas alterações aleatórias dos atributos-alvo. Subgrupos encontrados nessas cópias podem ser considerados aleatórios. Dessa forma, o método EPM foi aplicado sobre alguns datasets reais. O procedimento DFD permite controlar o problema das múltiplas comparações em SD e EMM, fornecendo uma forma robusta de identificar padrões realmente excepcionais enquanto minimiza a probabilidade de falsas descobertas.

O procedimento DFD tem apenas um parâmetro: o número de cópias do conjunto de dados. Este número deve ser suficientemente grande para satisfazer certas condições decorrentes da modelagem global envolvida na criação da DFD. Tipicamente, 100 cópias são suficientes, com um nível de significância estatística de 1%.

Seis bases de dados reais de diferentes domínios foram utilizadas nos experimentos. O dataset Algae apresenta os níveis de frequência de alguns tipos de alga em diferentes rios europeus. O dataset Sushi contém os dados demográficos de um conjunto de pessoas, bem como suas preferências em relação a diferentes tipos de sushi. O dataset Top7movies é um subconjunto de outra base de dados, que apresenta os rankings dos usuários para os 7 filmes mais avaliados. Os datasets GermanElections2005 e GermanElections2009 contém dados socioeconômicos dos distritos administrativos da Alemanha e o ranking de votação dos partidos mais populares nessas regiões. O dataset Cpu-small apresenta dados extraídos de medições relacionadas a servidores.

Filmes e sushi - Imagem gerada por DALL-E

Bases de Dados - Fonte: de Sá et. al, Table 2

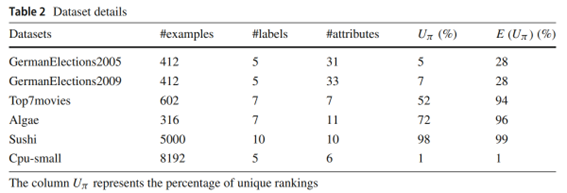
É usado um método chamado Regra de Distribuição para procurar distribuições alvo, ele foi comparado com o RWNorm aplicado no Cortana

Metodologia técnica DR - Fonte: de Sá et. al, Table 1

Para comparar a distribuição dos subgrupos com a populção (o conjunto de dados inteiro) foi realizado o teste estatístico de Komolgorov-Smirgov

Resultados obtidos

A excepcionalidade informada pelas métricas de qualidade podem se apresentar de diferentes formas em diferentes métricas de qualidade, ou seja, depende o que a métricas de qualidade está procurando. As métricas podem até estar correlacionadas, mas não perfeitamente, os autores forneceram no estudo uma forma do usuário utilizar essas métricas para tomar escolhas mais bem informadas.

Relação Entre Métricas de Qualidade - Fonte: de Sá et. al, Fig 2

A figura acima mostra geração de 10.000 subgrupos aleatórios, os quais a pontuação foi avaliada pelas métricas de qualidade apresentadas. A geração aleatória combina descrições até uma profundidade máxima ser alcançada. A profundidade da busca é fixada em 3, permitindo uma boa diversidade de combinações de atributos. Para cada par de métrica de qualidade na figura, há um scatter plot mostrando a relação das pontuações. A primeira linha mostra os subgrupos avaliados por RWNorm e o eixo vertical representa a pontuação dela; o eixo horizontal representa a pontuação de cada métrica de qualidade na seguinte ordem: RWNorm; RWNorm-mode; RWCov; LWNorm; PWMax

Pode-se notar que RWNorm-mode mostra um comportamento distinto, ela é baseada na matriz de distância diferencial L_S, obtida pela diferença entre as modas da população (M_D) e a moda dos subgrupos (M_S). Para essa métrica, se houver uma inversão de preferência no ranking dos rótulos em algum subgrupo de tamanho significativo, ele é considerado interessante, mesmo que seja pouco, como 2%. Para as métricas RWMNorm, LWNorm e PWMax, subgrupos desse tipo já não irão ser interessantes, a não ser que a diferença seja maior, isso fica evidente observando a segunda linha da Figura.

Observando o RWConv, parece que tem o maior viés, isso se dá pelo fato dessa métrica não se basear na matriz de distância L_S; ao invés disso ela é baseada na correlação negativa entre as matrizes de população (M_D) e subgrupos (M_S). Portanto, essa métrica de qualidade não necessariamente irá encontrar subgrupos que maximizem a preference distance, mas irá mostrar features não usuais de comportamento de forma abstrata.

1. Eleições Alemãs (2005 e 2009) GermanElections2005:

• Utilizando a métrica de qualidade PWMax com profundidade de busca 1, foram encontrados 62 subgrupos significativos.

• O subgrupo mais relevante foi “Região = Leste”, onde o partido Esquerda teve mais votos que o partido FDP em todos os 87 distritos da Alemanha Oriental, contrastando com a maioria dos distritos na Alemanha.

• Outro subgrupo significativo mostrou que em regiões de baixa renda (renda ≤ 16.979), o partido Esquerda recebeu mais votos que o partido Verde. GermanElections2009:

• Com as mesmas configurações, foram identificados 57 subgrupos significativos. Novamente, “Região = Leste” mostrou uma forte preferência pelo partido Esquerda em comparação ao partido Verde.

• Houve um aumento no número de distritos de baixa renda favorecendo o partido Esquerda em relação ao partido Verde comparado a 2005. Análise com LWNorm:

• Usando a métrica LWNorm com profundidade de busca 2, foram encontrados 2965 subgrupos significativos.

• O subgrupo “Região = Leste” continuou mostrando forte preferência pelo partido Esquerda.

• Outros subgrupos com características como menor população infantil e maior desemprego também favoreceram o partido Esquerda, enquanto regiões de maior renda mostraram o partido Esquerda como o menos votado.

2. Top7Movies

• Utilizando a métrica LWNorm, foram encontrados 2 subgrupos significativos com profundidade de busca 2.
• O primeiro subgrupo incluía pessoas com mais de 34 anos vivendo abaixo de uma latitude de 32.9, que não gostaram do filme “Beleza Americana” e preferiram “Star Wars: Episódio IV” e “O Resgate do Soldado Ryan”.
• A média de classificação deste subgrupo foi b (Star Wars: Episódio IV) > f (O Resgate do Soldado Ryan) > c (Star Wars: Episódio V) > d (Star Wars: Episódio VI) > g (O Exterminador do Futuro 2) > a (Beleza Americana) > e (Jurassic Park).

Resultados Filmes Matriz de Prefixos - Fonte: de Sá et. al, Fig 6

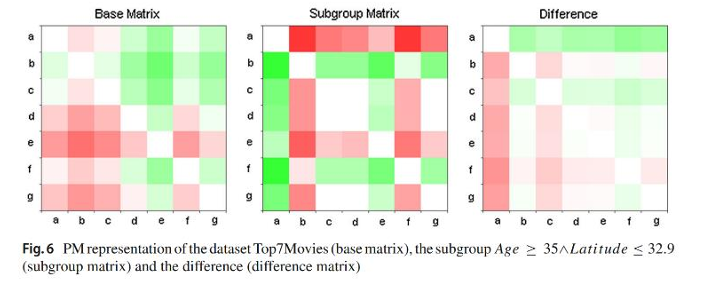
3. Algae

• Utilizando a métrica RWNorm, os resultados indicam que durante a primavera, as espécies de algas a, b e c são mais comuns em rios.
• A métrica LWNorm revelou mais de 400 subgrupos com profundidade máxima de 2.
• O melhor subgrupo mostrou que a espécie de alga a é fortemente preferida no subgrupo em comparação com o conjunto de dados geral.
• Utilizando profundidade de 3, foram encontrados cerca de 5400 subgrupos, mostrando um comportamento oposto em relação à espécie de alga a.

4. Sushi

• Devido ao alto percentual de rankings únicos, focou-se em padrões de ranking labelwise.
• A métrica LWNorm identificou 149 subgrupos.
• O melhor subgrupo revelou que homens com mais de 30 anos mostraram uma forte preferência por ouriço-do-mar (rótulo e), contrastando com a população geral.

Comparação de Subgrupod de Preferência de Sushi com a População - Fonte: de Sá et. al, Fig 10

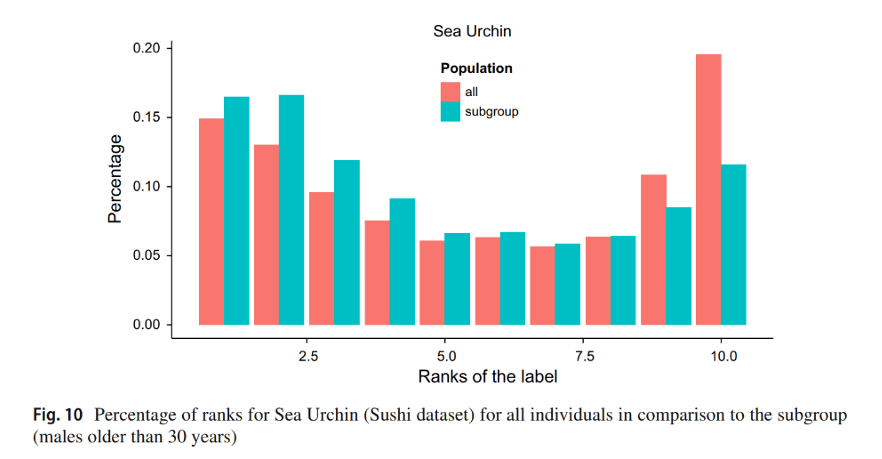
5. Cpu-small

• Utilizando a métrica RWCov, foram encontrados 275 subgrupos significativos com profundidade máxima de 4.
• O subgrupo mais relevante exibiu grandes desvios em todas as entradas da matriz de preferência, indicando comportamento de preferência incomum.

6. Comparação de Métricas de Qualidade

• Observou-se uma variação na quantidade de subgrupos obtidos por diferentes métricas.

• A RWNorm apresentou mais subgrupos em comparação a RWNorm-Mode e RWCov. Cada métrica mostrou diferentes vieses, destacando subgrupos específicos com comportamentos de preferência únicos.

• Esses resultados demonstram a eficácia do EPM na identificação de padrões de preferência excepcionais em diversos contextos, proporcionando insights valiosos sobre comportamentos não usuais em rankings.

Também foi feita uma comparação entre o CORTANA e o CAREN que usava a técnica DR:

Comparação Resultados CAREN vs CORTANA - Fonte: de Sá et. al, Table 5 & 6

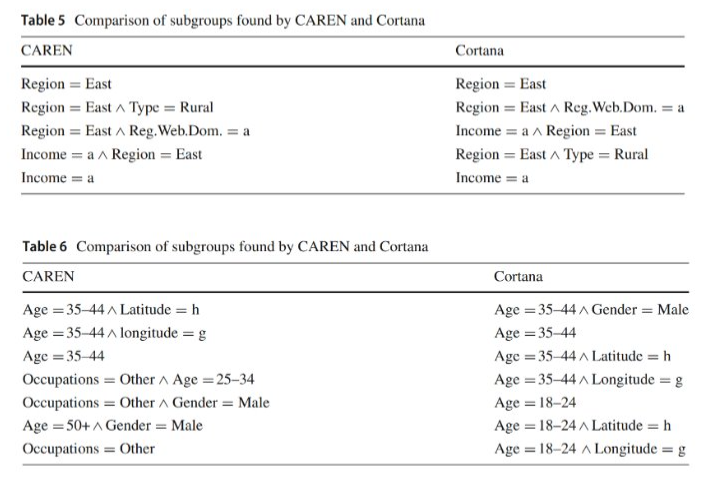
Aplicações e desafios

A mineração de preferências excepcionais pode ser aplicada em diversos contextos e trazer benefícios. Vamos apresentar abaixo algumas aplicações onde o uso de EPM teria grande valor.

Na área de negócios, seria possível encontrar subpopulações que possuem preferências divergentes da maioria, o que permitiria a construção de estratégias de marketing direcionado a esses nichos. Além disso, torna-se mais fácil a identificação de variações em tendências de mercado.

A medicina pode ser positivamente afetada pelo uso de EPM na segmentação de grupos de pacientes com características semelhantes. Isso faz com que cada grupo possa receber um tratamento mais especializado.

Outro exemplo de aplicação é o setor público. Nesse caso, o conceito de preferência poderia ser usado de forma análoga para identificar subgrupos que possuem necessidades específicas, possibilitando a criação de políticas públicas direcionadas para atender essas pessoas.

Na área de gestão de recursos humanos, seria interessante utilizar EPM para detectar nichos de funcionários que possuem alguns fatores de motivação e necessidades mais específicos. Assim, a equipe de RH poderia agir de maneira mais assertiva, tornando o ambiente de trabalho mais agradável e inclusivo.

Apesar das possibilidades benéficas citadas acima, é importante ressaltar os impactos negativos que podem surgir com a aplicação da técnica de EPM nesses cenários. O principal impacto identificado é a manipulação de informações. A busca por padrões de preferências que fogem à regra geral pode ser usada de forma indevida caso esses padrões sejam divulgados como se fossem representativos para toda a população. Como um exemplo, pode-se pensar no caso em que uma empresa usa as informações de grupos específicos para promover seus produtos para o público geral, o que configura em uma propaganda enganosa.

Execução dos algoritmos usados no artigo

O código-fonte desenvolvido pelos autores para elaboração do artigo não foi disponibilizado. No entanto, foram encontrados dois repositórios no GitHub que utilizam as mesmas técnicas e citam o artigo estudado.

Repositório MD2S_MusicProject

Este repositório não foi muito explorado pela equipe responsável, pois a documentação que explica os detalhes de implementação foi escrita em francês, o que dificultou o entendimento.

Link para o repositório

Repositório My-Sushi-Addiction

A implementação contida nesse repositório aplica a EPM em um dataset de preferências de tipos de sushi, mas permite também que outros datasets possam ser utilizados. Diferentemente do artigo, o algoritmo de busca usado nessa versão de EPM foi o beam search. No repositório, a métrica de qualidade é parametrizável, mas apenas a RWNorm está disponível para experimentação. Para utilizar outras métricas, é necessário implementá-las antes de passar como parâmetro.

Base de dados Sushi 2016

Link para o repositório

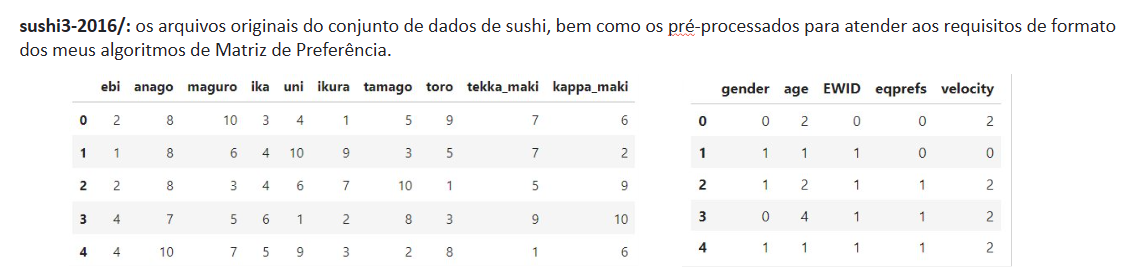
• 0 Quick_Start.ipynb: Realiza a execução do projeto em passos simples, bastando apenas seguir o roteiro do próprio notebook. É possível até aplicar a EPM aos próprios dados do usuário, não apenas ao dataset do sushi; ​

• 1 Exceptional_Preference_Mining.ipynb: Estruturado como um rascunho, este notebook mostra, passo a passo, como foi implementado o algoritmo de Beam Search e sua aplicação ao conjunto de dados de sushi;​

• beam_search.py: Funções para o algoritmo de Beam Search;​

• preference_matrix.py: Funções para calcular e visualizar a Matriz de Preferência, e calcular uma pontuação de excepcionalidade derivada delas.

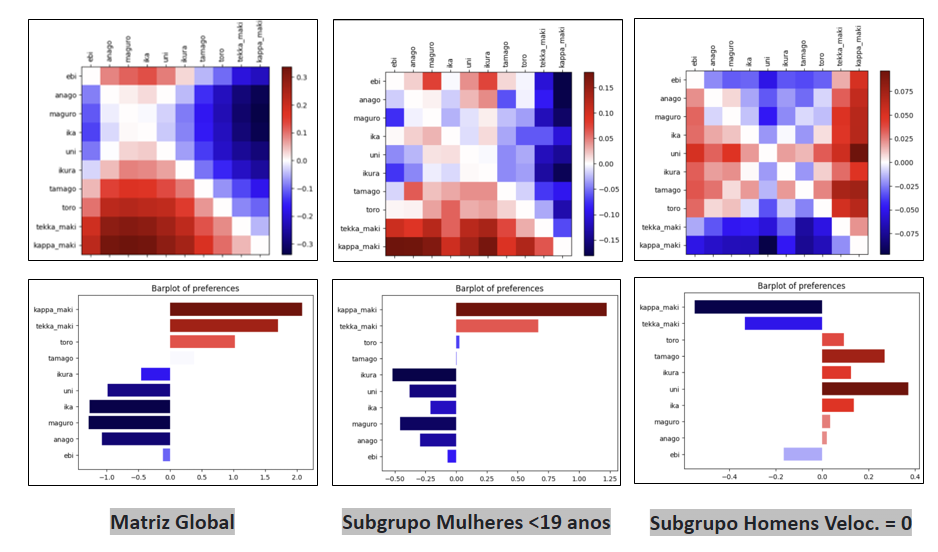
O grupo responsável realizou testes, aplicando o EPM sobre o dataset disponibilizado no repositório. Os principais subgrupos excepcionais descobertos foram os subgrupos de mulheres com menos de 19 anos e homens que responderam a pesquisa muito rapidamente. Também foram feitos experimentos com as outras métricas que não haviam sido previamente disponibilizadas. No geral, os resultados foram semelhantes àqueles vistos com a RWNorm. Uma descoberta notável foi o subgrupo de mulheres com menos de 39 anos de idade com a métrica LWNorm.

Resultados Hacker

Conclusão

O artigo analisado apresenta a técnica de Exceptional Preferences Mining (EPM) como uma abordagem inovadora para a descoberta de subgrupos com padrões de preferência excepcionais. Através de uma comparação detalhada com outras técnicas, como SD e EMM, o artigo evidencia a especificidade e a utilidade da EPM. Os experimentos realizados com diversos conjuntos de dados demonstram a eficácia da técnica e suas possíveis aplicações em áreas como negócios, medicina, setor público e gestão de recursos humanos. Apesar dos benefícios apresentados, é importante considerar os impactos negativos potenciais, como a manipulação de informações. A análise dos repositórios relacionados também fornece informações importantes sobre a implementação prática da EPM, evidenciando a adaptabilidade e flexibilidade da técnica.

Referências

de Sá, C. R., Duivesteijn, W., Azevedo, P., Jorge, A. M., Soares, C., & Knobbe, A. (2018). Discovering a taste for the unusual: exceptional models for preference mining. Machine Learning, 107, 1775-1807.