Artigo 5: For Real: A Thorough Look at Numeric Attributes in Subgroup Discovery
A descoberta de subgrupos (SD) é um método de mineração de dados que visa identificar padrões interessantes dentro de grandes conjuntos de dados, destacando segmentos específicos que diferem de forma significativa do restante. Este método é particularmente útil para explorar dados e encontrar subgrupos que apresentam comportamentos ou características notáveis.
No contexto da SD, os dados numéricos desempenham um papel crucial. Eles podem ser usados tanto como atributos de descrição, que ajudam a definir os subgrupos, quanto como alvos, onde se analisa o valor numérico em si. A forma como esses dados numéricos são tratados pode impactar significativamente a qualidade e a utilidade dos subgrupos descobertos. Com isso, é importante que a aplicação de métodos SD sejam adaptadas para lidar com esse tipo de dado da melhor forma possível.
Contextualização do problema
Historicamente, o tratamento de dados numéricos em algoritmos de descoberta de subgrupos tem sido predominantemente estático e global. Um exemplo disso é o mergeSD (2009), que abordou o tratamento de dados numéricos, embora com um aumento significativo no custo computacional. No entanto, muitos algoritmos clássicos ainda não tratam adequadamente os atributos numéricos, resultando na perda de informações relevantes e na diminuição da eficiência do modelo.
Para abordar essa questão, o artigo investiga qual abordagem é mais eficaz para lidar com esses atributos, utilizando um framework que compara diferentes estratégias de discretização de dados numéricos e de busca de subgrupos. A motivação central dos autores é compreender como a discretização dos valores numéricos pode ser realizada de maneira a preservar a qualidade e a redundância mínima nos subgrupos descobertos. Assim, o artigo pode ser visto como uma revisão dos principais métodos de tratamento de atributos numéricos em SD.
Conceitos importantes
A descoberta de subgrupos lida com atributos numéricos por meio de condições nos valores, discretizando-os em intervalos para tornar o problema tratável. A discretização pode ser realizada de forma global, no início do processo, com todos os pontos de corte definidos de uma vez, ou de forma local, sendo realizada dinamicamente durante a mineração.
Os intervalos gerados pela discretização podem ser binários ou nominais. Intervalos binários referem-se a divisões simples em duas categorias, como “baixo” e “alto”, enquanto intervalos nominais podem ter múltiplas categorias como “baixo”, “médio” e “alto”. No entanto, os autores mencionam que essa simplificação resultante da discretização pode descaracterizar os dados, pois os valores perdem certas propriedades ao serem agrupados em categorias. Por exemplo, ao comparar valores numéricos em um conjunto que varia de 1 a 10, os valores 7 e 8 podem ser categorizados como “alto”, fazendo com que 7 deixe de ser menor que 8, pois ambos são apenas “alto”.
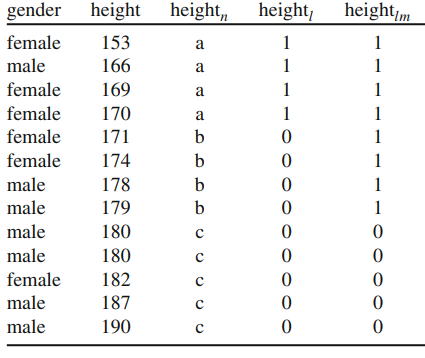
A tabela abaixo mostra um exemplo prático de discretização do atributo “height” (altura) de um grupo de 13 indivíduos usando a estratégia nominal e binária. Na estratégia nominal (coluna heightn), os pontos de corte foram definidos para os intervalos a ≤ 170 < b ≤ 179 < c. Já na estratégia binária temos duas categorias: low (coluna heightl) e low/medium (coluna heightlm) que correspondem a uma forma alternativa de discretizar os pontos de corte da estratégia nominal.
A granularidade para discretização refere-se ao nível de detalhe ou ao número de candidatos (intervalos) em que os dados numéricos são divididos. Granularidade fina envolve a criação de muitos intervalos pequenos, enquanto a granularidade grossa gera poucos intervalos maiores. Uma granularidade mais fina permite uma análise mais detalhada, mas pode aumentar o custo computacional. A seleção de candidatos pode incluir todos os possíveis subgrupos (all) ou apenas um subconjunto (best), o que também impacta o custo computacional.
Entendendo os algoritmos usados
Para dar suporte à investigação, os pesquisadores parametrizaram e executaram dois algoritmos de base: um para a descoberta de subgrupos e outro para a discretização de atributos numéricos.
O primeiro algoritmo, SDMM, realiza a busca de subgrupos válidos em uma base de dados, utilizando uma função de qualidade, restrições e estratégias de busca pré-estabelecidas. O algoritmo explora o dados, criando um primeiro subgrupo de busca e refinando o banco de dados a partir dele, com o objetivo de gerar novos candidatos para validação. Cada candidato é analisado, uma função de qualidade é associada a ele e é verificado se os candidatos seguem o padrão de qualidade estabelecido. Se sim, esses dados são adicionados ao conjunto solução; caso contrário, a busca é reiniciada.
O segundo algoritmo, Equal Frequency Discretisation, é um algoritmo de discretização que desenvolve intervalos de classe. No início do processo, é definido como os atributos numéricos serão discretizados, estabelecendo o número de intervalos de classes e, a partir desse número, o algoritmo define os pontos de corte das classes para categorizar os atributos.
Estratégias de busca
Para gerar os quadros de simulações possíveis e comparar as melhores soluções de descoberta de subgrupos, são utilizados três métodos principais: busca em feixe tradicional, busca em feixe CBSS e busca completa.
A busca em feixe tradicional é uma busca em nível, que limita o número de candidatos e a cada processamento. O método é ajustado para buscar subgrupos de acordo com um valor predefinido, restringindo o número de candidatos considerados em cada etapa.
A busca em feixe em CBSS é uma variação do feixe tradicional, que gera supercandidatos preliminares. Para otimizar a busca dos melhores candidatos, ele incrementa o número de candidatos, visando aumentar a diversidade do processo.
A busca completa realiza uma busca extensa usando todos os candidatos na busca de subgrupos. Embora isso aumente a qualidade da descoberta, há um custo operacional elevado e redundância. Trabalhar com grandes bancos de dados pode ser difícil e, apesar de melhorar a qualidade, a performance pode ser prejudicada.
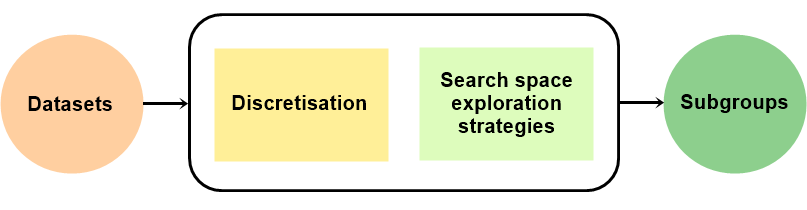
Metodologia
No que diz respeito à metodologia do artigo, os autores realizaram uma série de testes, com todas as combinações de hiperparâmetros e estratégias possíveis. Ao todo, forma avaliados 5 aspectos diferentes de SD e como cada um deles impacta os resultados, são estes:
- Hiperparâmetros, que se dividem em 2 tipos:
- Número de bins: quantidade de quebras na discretização.
- Profundidade: número de descritores.
- Estratégias para o SD numérico que variam em 4 dimensões, havendo duas opções para cada e, portanto, 2^4 possibilidades:
- Momento de discretização (local ou global).
- Tipo de intervalo (binário ou nominal).
- Granularidade (fina ou grossa).
- Métodos de seleção (“all” ou “best”).
- Datasets utilizados, que podem ser para dois tipos de problemas:
- Datasets de classificação e regras não supervisionados, ex: covertype, credit-a, outros.
- Datasets de regressão, ex: auto-mpg, abalone, outros.
- Estratégia de busca:
- Complete search: envolve a exploração de todo o espaço de busca.
- Beam search: limita o número de candidatos a cada nível da busca.
- Beam search + CBSS: otimização para tentar reduzir a redundância dos subgrupos.
- Métricas de avaliação:
- WRAcc: para classificação.
- z-score: para regressão.
- Entropia conjunta: para calcular a redundância dos top 10 subgrupos.
Para avaliar esses aspectos, foram realizados 17.020 experimentos, utilizando o algoritmo SDMM. Os experimentos utilizaram seis datasets de classificação e seis datasets de regressão e foram avaliados através de WRAcc para classificação e |z-score| para regressão.
Resultados obtidos
As conclusões sobre vários aspectos obtidas com os resultados dos experimentos podem ser vistas de forma resumina no quadro a seguir:
| Aspecto metodológico | Conclusão |
|---|---|
| Discretização | Não existe regra universal para o número de bins. Estratégias nominais têm melhor desempenho com números de bins menores, mas estratégias binárias são preferíveis em todos os contextos e aplicações. A discretização local é sempre melhor. |
| Busca | A escolha da heurística de busca tem pouco impacto. Beam search é recomendada por ser eficiente e apresentar resultados bons quanto à complete search. Em datasets pequenos, a busca completa pode ser útil. CBSS reduz a redundância, mas não melhora a qualidade. |
| Métricas de Qualidade | As métricas impactam significativamente nos subgrupos gerados, especialmente nos tamanhos, favorecendo subgrupos maiores. Avaliação feita com a correlação de Pearson. |
| Granularidade | A granularidade fina é melhor, mas em grandes profundidades, granularidades fina e grossa são equivalentes. |
| Método de Seleção | O método “all” é melhor, mas o “best” melhora a eficiência sem grandes perdas de qualidade. |
No artigo, as estratégias utilizadas são denotadas por siglas que combinam várias letras, cada uma representando um hiperparâmetro específico da metodologia aplicada. Abaixo segue uma explicação simplificada do que cada letra nas iniciais das estratégias representa:
- L: Refere-se ao uso de discretização local.
- G: Refere-se ao uso de discretização global.
- B: Indica o uso de intervalos binários.
- N: Indica o uso de intervalos nominais.
- F: Representa a abordagem de granulidade fina na discretização dos dados.
- C: Representa a abordagem de granulidade grossa na discretização dos dados.
- A: Refere-se à categoria All no método de seleção.
- B: Refere-se à categoria Best no método de seleção.
Assim, por exemplo, uma estratégia LBFA aplica discretização local com intervalos binários, granularidade fina e método de seleção “all”.
Por fim, os autores apresentaram uma tabela dos resultados com as melhores escolhas para as 4 dimensões de estratégias em forma de ranking. Essa tabela se divide em duas partes, a primeira coluna que é baseada apenas na avaliação do melhor subgrupo gerado e a segunda leva em conta os 10 melhores subgrupos.
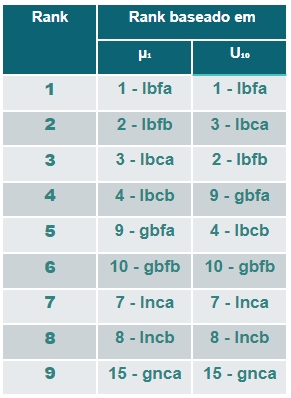
De modo geral, os melhores resultados foram obtidos pelas estratégias LBFA e LBFB. Entretanto, esse ranking geral não tem garantia de estatística, visto que ele foi criado a partir de uma combinação de vários testes.
Vale ressaltar que uma estratégia em particular (LXFB) também apresentou resultados bons mas se distingue das demais por usar intervalos cartesianos como técnica de discretização, ao invés dos binários ou nominais. Devido às suas limitações de aplicabilidade, ela foi testada separadamente e teve performance melhor que todas as demais, sendo a melhor estratégia quando o objetivo principal é obter subgrupos de alta qualidade para classificação. No entanto, ela não é aplicável para regressão.
Aplicações e desafios
A descoberta de subgrupos com atributos numéricos tem diversas aplicações, como por exemplo nas áreas da saúde, educação e setor financeiro. No entanto, também apresenta desafios específicos em cada uma dessas áreas.
Na saúde, os modelos podem ser utilizados para predição de riscos, identificando subgrupos de pessoas mais suscetíveis a doenças de alto risco. Além disso, são úteis na análise de resposta a tratamentos, permitindo encontrar subgrupos que reagem de forma diferenciada a determinadas terapias, e no controle de doenças crônicas, identificando subgrupos que necessitam de cuidados específicos. Outra aplicação interessante é o mapeamento de áreas de risco em uma cidade, identificando regiões negligenciadas pelo sistema de saúde, que necessitem de maior atenção e investimento.
Na educação, os modelos de descoberta de subgrupos podem ser aplicados para melhorar a performance acadêmica, identificando subgrupos de alunos com características similares para personalizar a abordagem pedagógica. Outra aplicação potencial é a predição de desistência, onde é possível identificar subgrupos de alunos com maiores índices de evasão, e assim, oferecer medidas de apoio adequadas. Adicionalmente, é possível identificar áreas de risco educacional, destacando regiões com baixo investimento em educação para criação de novas políticas públicas que visem melhorar a qualidade do ensino nessas áreas.
No setor financeiro, os modelos podem ser utilizados para otimização de portfólio, identificando subgrupos de ações que melhor se encaixam no perfil de determinados investidores. Além disso, também podem ser empregados na detecção de fraude, identificando subgrupos de transações que apresentam características anômalas. Na análise de crédito, é possível identificar subgrupos de pessoas com maior propensão a cometer fraudes bancárias, a fim de adotar medidas preventivas.
Apesar dos benefícios das diversas aplicações, a descoberta de subgrupos com atributos numéricos apresenta desafios comuns nas três áreas discutidas. A privacidade dos dados é uma preocupação constante, sendo necessário garantir o controle sobre onde os dados, como serão utilizados e quem pode acessá-los. A discriminação e a equidade de tratamento também são questões importantes, uma vez que a identificação de subgrupos pode gerar preferência de tratamento para determinados grupos, prejudicando outros.
Execução dos algoritmos usados no artigo
Dois repositórios podem ser destacados para a execução do código proposto para análise de algoritmos de descoberta de subgrupos. O primeiro repositório é o da Universidade de Leiden, que disponibiliza o sistema Cortana. Esse sistema possui tanto o código-fonte quanto o binário compilado para execução. A página oficial do Cortana fornece informações gerais sobre a ferramenta e o binário pode ser baixado diretamente da página disponibilizada. Além disso, o código-fonte está disponível para desenvolvedores que desejam explorar ou modificar o sistema.
O Cortana se destaca pela sua documentação extensa, encontrada no diretório /javadoc do código-fonte. No entanto, apresenta uma limitação significativa: a falta de um histórico de atualizações e uma descrição detalhada das funções. Isso pode dificultar a compreensão completa do sistema e a rastreabilidade de mudanças ao longo do tempo, o que é crucial para desenvolvedores e pesquisadores que precisam entender a evolução do software.
O segundo repositório discutido foi o SubDisc, disponível no GitHub e atualizado regularmente, com a última atualização registrada em 12 de outubro de 2023. O SubDisc é escrito em Java e se foca principalmente na usabilidade e interface do usuário. Uma das grandes vantagens desse repositório é a inclusão de um guia detalhado em PDF, que fornece instruções claras sobre como utilizar a ferramenta, tornando-a acessível mesmo para aqueles que não são especialistas na área.
A qualidade dos repositórios varia, mas ambos têm suas particularidades e utilidades. O Cortana, apesar de sua documentação extensa, carece de detalhes históricos e descrições de funções, o que pode ser um desafio. Por outro lado, o SubDisc se sobressai com sua documentação voltada para o usuário final e um guia de uso detalhado, embora não haja menção à profundidade da documentação técnica. A escolha entre essas ferramentas dependerá das necessidades específicas dos usuários, seja para um entendimento profundo do funcionamento interno ou para uma interface de usuário amigável.
Um teste foi realizado utilizando a ferramenta Cortana. O dataset utilizado, tanto para regressão, quanto para classificação, foi o Adult, do repositório de Machine Learning da UCI. Na tarefa de classificação, o foco foi buscar subgrupos que apresentam um comportamento diferente da população em relação à variável binária “renda anual ≥ 50k”. Na tarefa de regressão, o foco está na idade dos indivíduos, verificando se há subgrupos com uma distribuição de idade atípica em relação à população geral.
Para instalar o Cortana, baixe o arquivo cortana1782.jar e execute-o com o comando java abaixo na linha de comando.
java -jar cortana1782.jarApós iniciar o programa, selecione o arquivo de dados nos formatos arff ou csv, ajuste os parâmetros conforme o tipo de objetivo (por exemplo, Single Numeric ou Single Nominal) e as medidas de qualidade desejadas (como Lift ou Z-Score). Verifique se os dados foram identificados corretamente e ajuste os tipos de atributos, desabilitando colunas indesejadas. Configure o método de descoberta, definindo parâmetros como profundidade de refinamento e cobertura mínima e máxima, e utilize a estratégia de beam search com um tamanho de beam de 100. Clique no botão “Subgroup Discovery” para iniciar o processo.
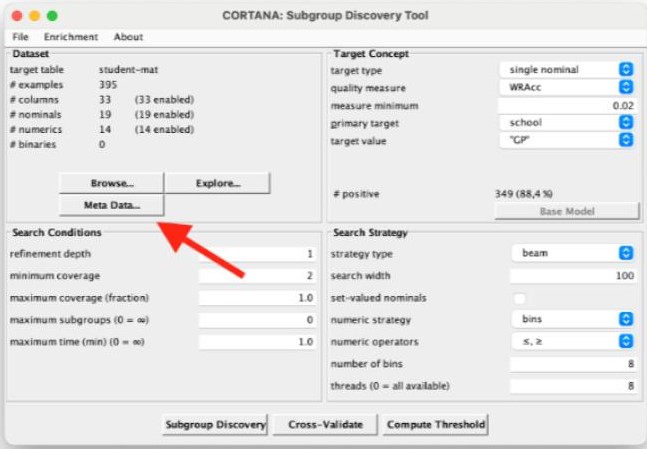
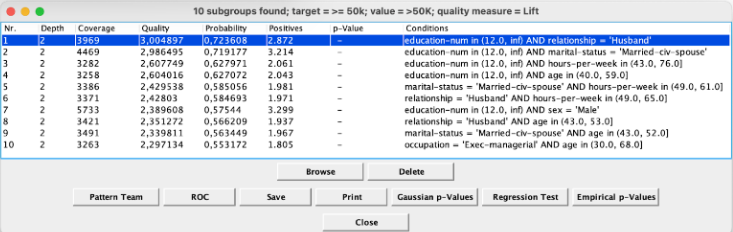
No primeiro exemplo, para um problema de classificação onde se deseja identificar pessoas com renda anual ≥ 50k, foi configurado o método como Beam Search, com largura do beam de 100, profundidade de refinamento de 2, métrica de qualidade Lift (≥ 1.0) e cobertura entre 10% e 90%. Após selecionar o arquivo adult.csv e ajustar os parâmetros e atributos, a execução do algoritmo resultou em subgrupos como “education-num > 12.0 AND capital-gain > 5000”, com uma AUC de 0.85 na curva ROC.
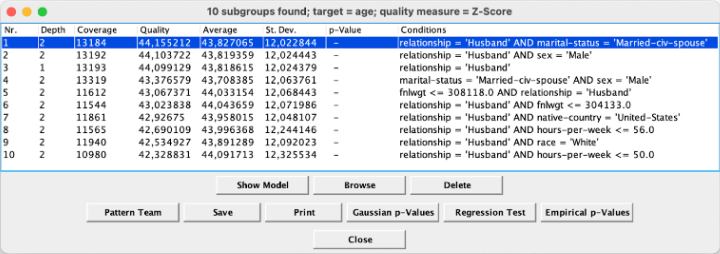
No segundo exemplo do problema de regressão, para identificar distribuições não usuais de idade, a configuração também incluiu Beam Search, com largura do beam de 100, profundidade de refinamento de 2 e cobertura entre 10% e 90%. Todavia, a métrica de qualidade foi Z-Score (≥ 2.0). A execução encontrou subgrupos como “relationship = husband AND hours-per-week > 40”, permitindo a comparação da distribuição de idade com a população geral.
Conclusão
O trabalho cumpre um papel importate na realização de experimentos capazes de confirmar algumas intuições não validadas até então e aprimorar o conhecimento em relações a estratégias numéricas. Nesse sentido, é um estudo bastante útil tanto em uma perspectiva aplicada, podendo servir como apoio na decisão de aspectos em aplicações reais, quanto no contexto de pesquisas e desenvolvimento de algoritmos.
Referências
Boley M, Goldsmith BR, Ghiringhelli LM, Vreeken J (2017) Identifying consistent statements about numerical data with dispersion-corrected subgroup discovery. Data Min Knowl Discov 31(5):1391–1418. https://doi.org/10.1007/s10618-017-0520-3.