Artigo 1: A Survey of High Utility Itemset Mining

No campo da mineração e análise de dados, a mineração de padrões frequentes possui uma relevância bastante significativa, sendo importante para encontrar associações e correlações entre diferentes variáveis. Essa área de estudo surgiu juntamente com o crescimento exponencial da quantidade de dados disponíveis em diversos setores da vida cotidiana, em especial o comércio, tendo sido batizada com o nome de “Analise da cesta de compras”.

Ilustração da análise de cesta de compras.

Para dar seguimento a este artigo, é necessário definir (ou relembrar) alguns conceitos:

Item: Um item é todo elemento de interesse que possui significado próprio e pode ser associado a n outros itens formando um padrão, ou conjunto. Para a mineração de padrões frequentes, é definido um universo finito dos itens na área em que se deseja empregar a técnica. Um item pode ser, por exemplo, uma garrafa de água no contexto de análises de comércio, ou uma ação tomada no contexto de análises comportamentais.
Transação: Uma transação é uma coleção de itens que foram adquiridos em conjunto de uma única vez, por uma única pessoa. O conjunto de transações é o que forma a base de dados utilizada para a análise, sendo que em quanto mais transações um padrão ocorrer, mais frequente ele é.
Padrão (Itemset): Os padrões são o que se espera encontrar ao fim do algoritmo, eles são conjuntos de itens (itemsets) que ocorrem dentro das transações, podendo englobar todos os itens de uma transação, ou ser um subconjunto dela.
Suporte mínimo: O suporte mínimo é a quantidade mínima de vezes que um padrão deve ocorrer nas transações para que ele seja considerado frequente.

A análise final dos padrões identificados como frequentes através da mineração executada pode muitas vezes ser complicada, por se tratar de uma técnica de aprendizado não supervisionado. Mas além da complexidade inata da análise de resultados, existe também a possibilidade dos padrões obtidos não significarem nada, ou simplesmente serem pouco úteis para os objetivos do negócio.

Por exemplo, considere que na análise de uma papelaria os itens “lápis” e “borracha” são frequentemente incluídos em uma mesma transação, o preço final pago pelo consumidor por apenas esse conjunto de itens será muito baixo, não trazendo os benefícios esperados da análise. Porém, na mesma papelaria, pode ser que os itens impressora e cartucho de tinta também são frequentemente comprados juntos, o que leva a um preço final maior pago pelo consumidor.

Comparação entre padrões frequentes e padrões úteis.

O exemplo anterior é básico, mas ilustra a ideia de que os itens serem apenas frequentes pode não ser o suficiente, sendo necessário que as combinações analisadas sejam também úteis para o analista. É nesse contexto que surge a mineração de padrões frequentes de alta utilidade, tratada no artigo “A Survey of High Utility Itemset Mining”, que aborda diferentes algoritmos para resolver esse problema.

Para entender esses algoritmos, é primeiro necessário fazer uma segunda leva de definições sobre o assunto, dessa vez mais específicas ao escopo de mineração de padrões de alta utilidade:

Utilidade interna: Se refere à utilidade de um item quando comparado com os outros dentro de uma mesma transação, podendo ser contabilizada como a quantidade de ocorrências daquele item dentro da transação. Note que essa medida é específica para cada uma das transações, com um item podendo ter uma alta utilidade interna em uma e uma baixa em outra.
Utilidade externa: Se refere à utilidade de um item quando comparado com todos os outros itens em um âmbito mais geral, podendo ser representado como o preço dele, o peso, ou outra medida importante.
Utilidade total do item: Calculada como a multiplicação da utilidade interna e externa do item na transação em específico.
Utilidade total do padrão (itemset): Calculada como a soma da utilidade total de todos os itens que componham o padrão, note que se um item não está presente em uma transação, a utilidade total dele automaticamente é zero.

Ilustração das utilidades.

Perceba que, de acordo com essas definições, todos os algoritmos que são utilizados para mineração de padrões frequentes de alta utilidade podem também ser utilizados para minerar padrões frequentes, basta que a utilidade interna e externa de todos os itens seja definida com o mesmo valor, preferencialmente “1”. Para entender melhor as semelhanças e diferenças entre as duas técnicas de mineração de dados, verifique a tabela a seguir:

Semelhanças Diferenças
Objetivo: ambas as técnicas buscam Medida de importância: na mineração de
identificar padrões significativos em grandes itens frequentes, a importância é medida pela
conjuntos de dados para auxiliar decisões de frequência; na de alta utilidade,
negócios. considera-se o valor econômico ou estratégico
dos itens (função de utilidade).
Limite mínimo: ambas utilizam a ideia de Complexidade algorítmica: algoritmos de
limiar mínimo para filtrar padrões alta utilidade são mais complexos devido à
significativos. ausência de propriedades de monotonicidade,
que são úteis na mineração de itens
frequentes para reduzir o espaço de busca.
Processamento de dados: as duas técnicas Aplicações: a mineração de itens de alta
operam frequentemente sobre dados utilidade é ideal em cenários onde a
transacionais, que registram itens associados maximização do lucro e utilidade dos itens é
conjuntamente. essencial, enquanto a mineração de itens
frequentes se aplica melhor a análises de
co-ocorrência de itens de interesse.
Redução de dimensionalidade: ambas as
abordagens reduzem o espaço de busca
eliminando itens que não atendem aos critérios
mínimos.

Técnicas e Algoritmos usados

O artigo estudado tem por objetivo apresentar a área de mineração de padrões frequentes de alta utilidade, além de mostrar ao leitor diferentes algoritmos para realizar essa mineração. As principais técnicas para a confecção dos algoritmos são a de “Duas fases” e de “Uma fase”, essas técnicas serão explicadas nas próximas subseções, juntamente com um algoritmo representante de cada classe.

Algoritmos de duas fases

Algoritmos que seguem essa técnica usam o conceito de “Utilidade da transação”, ou Transaction Utility (TU), que pode ser definido como a soma da utilidade de todos os itens que estão presentes em uma transação, para definir limites superiores do quão alta a utilidade de um subconjunto dessa transação pode ser. Esse limite superior é calculado para cada um dos padrões (itemsets) candidatos através de uma “Utilidade com peso em transações”, ou Transaction Weighted Utility (TWU), que é definida como a soma da utilidade de todas as transações que contêm o padrão em evidência.

O valor obtido de TWU para um itemset, é o limite superior para todos os superconjuntos que possam ser formados a partir dele. Por exemplo, suponha a existência de um itemset base {a, b} que possui TWU igual a 10, isso significa que qualquer itemset da forma {a, b, _}, onde o terceiro e último item pode ser qualquer um do universo de itens disponívei, terá necessariamente uma utilidade menor que 10. A aplicação dessa propriedade nos algoritmos traz um importante avanço, que é o estabelecimento de um decrescimento monotônico do TWU de acordo com o aumento dos itens em um itemset.

A partir dessas propriedades, é definido um suporte de utilidade mínimo que elimina todos os itemsets que tenham TWU abaixo desse limiar assim que são identificados, evitando a geração de superconjuntos que não têm chances de serem de alta utilidade.

Exemplo de cálculo do TWU.

A primeira fase dos algoritmos consiste em gerar o TWU de todos os itens disponíveis, já que eles são o menor itemset possível (excluindo o conjunto vazio). Após o cálculo, todos os itemsets unitários que tenham um TWU que estejam abaixo do suporte de utilidade mínimo definido são eliminados do espaço de busca, evitando que candidatos infrutíferos sejam gerados. Em seguida, a geração de candidatos continua para os itemsets de dois elementos gerados a partir dos remanescentes do filtro anterior, sendo que esses novos candidatos serão também removidos no caso de terem TWU menor que o suporte mínimo. Essa sequência de ações continua em repetição até que já não seja mais possível gerar novos candidatos.

Note que nessa primeira fase está sendo calculado o TWU, que é o limite superior de utilidade, e não a utilidade dos itemsets em si

A segunda fase do algoritmo consiste em calcular a utilidade de todos os candidatos que sobraram da fase anterior, eliminando aqueles que tenham utilidade menor que o limite inferior estabelecido.

O primeiro algoritmo desenvolvido para essa técnica se chama Two-Phase Algorithm, tendo sido baseado no algoritmo Apriori para mineração de padrões frequentes. É possível ver uma imagem do pseudocódigo desse algoritmo a seguir:

Pseudocódigo do algoritmo Two-Phase.

Perceba que a função ITEMSETGENERATION() recebe apenas o conjunto de candidatos da iteração anterior como parâmetro, não verificando a base de dados de transação para gerar os candidatos, o que pode levar a itemsets que não ocorrem em nenhuma transação, resultando em um desperdício de tempo considerável para os cálculos deles.

Outra limitação do algoritmo é que ele itera pelo conjunto de dados várias vezes para calcular o TWU dos itemsets, elevando o custo do algoritmo. Note que a exploração do espaço de busca desse algoritmo segue a técnica de Breadth First Search (BFS), o que leva a uma maior demora para eliminação de candidatos infrutíferos, principalmente pelo fato de que o TWU é uma métrica de limite extrapolada.

Algoritmos de uma fase

Esses algoritmos são mais diretos, fazendo o cálculo da utilidade de cada padrão considerado no espaço de busca, o que permite identificar imediatamente se um itemset é de alta ou baixa utilidade sem a necessidade de guardá-lo em memória principal (RAM).

Outra novidade desses algoritmos é que eles trazem uma nova forma de calcular os limites superiores de utilidade, sendo mais próxima à utilidade real dos itemsets do que o TWU usado nos algoritmos de duas fases. Como exemplo de algoritmo dessa técnica, será utilizado o Fast High-Utility Miner (FHM), que introduz o conceito de Listas de Utilidade, ou Utility List (UL), para representar o banco de dados das transações.

Considerando um itemset X, a lista de utilidade UL(X) será uma lista de tuplas para todas as ocorrências de X nas transações do banco, sendo que cada tupla armazenará o ID da transação em que o itemset está presente, a utilidade do itemset naquela transação e a soma da utilidade de todos os itens com ordem lexicográfica superior aos itens de X. O algoritmo se inicia calculando as listas de utilidade de todos os itemsets de um único elemento, sendo que as listas de utilidades dos superconjuntos desses itemsets será calculada a partir dos componentes delas.

Por exemplo, suponha as listas de utilidade dos conjuntos unitários UL({a}) e UL({d}), para gerar a lista de utilidade e calcular a utilidade do itemset {a, d}, será calculada a interseção das transações que estão em UL({a}) e UL({d}). A utilidade do novo itemset será simplesmente a soma das utilidades dos itemsets geradores, enquanto a utilidade dos itens com ordem lexicográfica superior será igual a presente no itemset gerador de maior ordem lexicográfica, no caso do exemplo, será o mesmo de {b}.

Exemplo de cálculo das listas de utilidade.

O cálculo do limite superior para esse algoritmo é chamado de “Limite Superior por Utilidade Residual”, ou Remaining Utility Upper-Bound, é feito somando a utilidade de um item (iutil) com a utilidade dos itens residuais de ordem lexicográfica maior (rutil) para todas as transações presentes na lista de utilidade. Caso esse resultado final seja menor que a utilidade mínima definida, aquele itemset é eliminado do espaço de busca, evitando que novos candidatos sejam gerados. A figura a seguir mostra o pseudocódigo para o algoritmo FHM:

Pseudocódigo do algoritmo FHM.

Algoritmos baseados em listas de utilidade, como o FHM, são até duas ordens de magnitude mais rápidos que os algoritmos de duas fases. Porém, a geração de candidatos ainda é baseada em itemsets anteriores, sem verificar o banco de dados de transações, o que pode levar a candidatos inexistentes e aumento no custo total do algoritmo por gastar recursos verificando possibilidades desnecessárias.

Além disso, o custo de memória para o armazenamento das listas de utilidade de cada itemset verificado pode vir a ser preocupante. Outro ponto de atenção de algoritmos que seguem essa estratégia é o fato de que são feitas muitas comparações com listas de utilidade anteriores no processo de geração de candidatos, já que um candidato com k itens deverá fazer comparações com k-1 listas de utilidade anteriores.

Metodologia do artigo

O artigo adota uma abordagem metodológica baseada em Survey, delineando inicialmente o problema em questão e, em seguida, apresentando algoritmos destinados à sua resolução. Uma filtragem criteriosa de artigos relevantes no domínio da mineração de itemsets de alta utilidade foi realizada, seguida pela compilação e síntese dos algoritmos destacados, abordando suas estruturas e conceitos fundamentais.

Os primeiros algoritmos abrangentes para identificar conjuntos de itens de alta utilidade operam em duas fases distintas: primeiro, geram-se candidatos que são subsequentemente avaliados quanto à sua utilidade efetiva. Esses algoritmos introduziram uma inovação crucial ao estabelecer uma medida monótona que serviria como limite superior para a utilidade dos conjuntos de itens. Uma dessas medidas pioneiras foi a TWU (Transaction-Weighted Utilization), a qual permitiu uma poda eficiente do espaço de busca. Em estágios posteriores, surgiram algoritmos de uma única fase, cujo propósito é economizar tempo ao integrar a geração e avaliação de candidatos em um único passo. Vale ressaltar que muitos desses algoritmos propostos representam generalizações de técnicas de mineração de conjuntos de itens frequentes estabelecidas, como o Two Phase (uma extensão do Apriori) e o UP-Growth (uma extensão do FP-Growth).

Dentre os algoritmos apresentados para a mineração de padrões frequentes de alta utilidade são destacados os seguintes:

Algoritmo Tipo de Busca Fases Representação dos Dados Extende
Two-Phase Busca em Largura Duas Horizontal Apriori
HUP-Growth Busca em Profundidade Duas Horizontal (Árvore de Prefixos) FP-Growth
D2HUP Busca em Profundidade Uma Vertical (Hiperestrutura) H-Mine
FHM Busca em Profundidade Uma Vertical (Listas de Utilidade) Eclat
EFIM Busca em Profundidade Uma Vertical (com fusões) LCM

O artigo porém não se contém somente em discutir os algoritmos completos de mineração de padrões, mas também, reconhecendo a importância de representações com um nível maior de significado. É nesse ponto em que são apresentados os algoritmos que mineram representações concisas dos subconjuntos de alta utilidade:

Algoritmo Padrões Fases Representação dos Dados Extende
MinFHM MinUIs Uma Vertical (Listas de Utilidade) FHM
CHUD CHUIs Duas Vertical (Listas de Utilidade) DCI Closed
EFIM-CLOSED​ CHUIs Uma Horizontal (com fusões) EFM
GUIDE MHUIs One Uma Stream UpGrowth

Por fim, são apresentados algoritmos que retornam apenas os K subconjuntos de alta utilidade mais frequentes no conjunto de transações:

Algoritmo Tipo de Busca Fases Representação dos Dados Extende
TKU​ Busca em Profundidade​ Duas Horizontal (Árvore de Prefixos) ​ UP-Growth​
TKO​ Busca em Profundidade​ Uma Vertical (Listas de Utilidade) HUI-Miner​
REPT​ Busca em Profundidade​ Uma Horizontal (Árvore de Prefixos)​ MU-Growth​
kHMC​ Busca em Profundidade​ Uma Vertical (Listas de Utilidade)​ FHM​

Aplicações e Desafios Éticos e Sociais

Há uma vasta gama de problemas do mundo real que podem se beneficiar significativamente do uso de algoritmos de mineração de subconjuntos frequentes de alta utilidade. Entre eles:

  • Mercado de Varejo: Potencial para aumentar os lucros ao impulsionar as vendas de produtos mais rentáveis.
  • Mercado de Compra Conjunta: Oportunidade de melhorar a lucratividade ao associar produtos visando redução de impostos.
  • Sistema de Recomendação: Aprimoramento da capacidade de gerar lucro ao focar em produtos mais rentáveis.
  • Cross-Selling e Up-Selling: Estímulo para compras de produtos complementares e promoção de vendas casadas.
  • Tratamento de Saúde: Desenvolvimento de conjuntos de tratamentos visando maior eficiência.
  • Detecção de Fraudes: Identificação de padrões pouco frequentes, porém altamente úteis, na detecção de fraudes. Uso da Internet:__ Análise do comportamento dos usuários para aprimorar a importância do site.
  • Telecomunicações: Utilização na identificação de padrões de comunicação que resultam em maior lucratividade.
  • Mineração de Texto: Identificação de textos com elevado valor agregado.

No entanto, a implementação de algoritmos de mineração de alta utilidade suscita preocupações sociais e éticas que demandam uma atenção cuidadosa. Um ponto crucial é a ameaça à privacidade, uma vez que a identificação de indivíduos a partir de dados aparentemente anônimos pode comprometer a segurança dos mesmos. Ademais, há o risco de manipulação do mercado e do comportamento do consumidor, onde o conhecimento de padrões de consumo pode ser utilizado de maneira indevida para influenciar escolhas.

Outra questão relevante é a elisão fiscal, na qual empresas utilizam o conhecimento de padrões de alta utilidade para minimizar suas obrigações fiscais de forma legal, mas questionável do ponto de vista ético. Esses desafios destacam a importância de regulamentações sólidas e transparência no uso de algoritmos de mineração de dados, garantindo que o impacto social e ético seja considerado em todas as etapas, desde a implementação até a operação dessas ferramentas avançadas.

Como usar

Neste guia iremos ensinar o passo a passo para poder executar o SPMF, um software livre que tem implementado vários algoritmos de mineração de itemsets de alta qualidade.

A execução do SPMF exige o JAVA versão mínima 1.8, aqui iremos mostrar a instalação tanto do JAVA quanto do SPMF para o Windows, o processo de instalação do programa deve ser o mesmo no Linux, já que o programa é baseado em JAVA, a diferença se dará na instalação do JAVA.

Instalação

Inicialmente segui o guia de instalação do JAVA deste link, mas na hora de execução do SPMF o programa não funcionou e a solução foi reinstalar o JAVA de outra forma. Apenas a fim de documentar um possível erro que você encontre ao tentar executar o SPMF, fica aqui o vídeo do processo de instalação que não funcionou.
Instalação da versão errada do JAVA
A instalação do SPMF é simples e se encontra neste link. O vídeo a seguir mostra o processo inteiro:
Instalação do software SPMF
Como dito anteriormente, no final obtemos um erro do JAVA que é concertado pela re-instalação de uma versão atual neste link, tal processo é mostrado no vídeo a seguir:
Instalação da versão mais recente do JAVA

Execução

Arquivo de Entrada

O SPMF suporta arquivos de entrada no formato .txt.

A primeira parte do arquivo de entrada é opcional e é usada para nomear os itens presentes no banco de dados.

  • Linhas começando com @​.
  • Primeira linha com “@CONVERTED_FROM_TEXT”​
  • Demais linhas fazem a ligação do item com sua descrição no formato @ITEM={ID}={DESCRICAO}
    • {ID} é o número do item
    • {DESCRICAO} é o nome do item
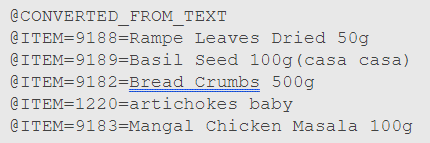
Primira parte do arquivo de entrada (opcional)

A segunda parte contém os dados das transações, com cada linha representando uma transação e cada coluna separada por “:” contendo o itemset, a utilidade total do itemset e a utilidade de cada item do itemset, respectivamente.

  • Linhas representam as transações​
  • Cada linha possui 3 colunas separadas pelo caractere ‘:’​
    1. Coluna 1: itemset com os ids dos itens separados por espaço simples.
    2. Coluna 2: utilidade total do itemset.
    3. Coluna 3: utilidade respectiva de cada item do itemset separadas por espaço simples.​
Segunda parte do arquivo de entrada

Execução do Software

Vídeo tutorial de como se deve executar o programa a partir do dado de entrada, o algoritmo escolhido no tutorial foi o Two-Phase:

Apesar de no tutorial ser mostrado a execução com o algoritmo Two-Phase, temos várias opções de algoritmos para mineração de itensets de alta utilidade, como UP-Growth, UP-Growth+, FHM e HUI-Miner.

Arquivo de Saída

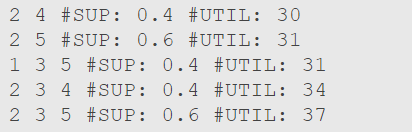
A saída do algoritmo também é um arquivo .txt, contendo os itemsets de alta utilidade encontrados, o suporte do itemset (nem todos os algoritmos geram esse valor) e a utilidade do itemset.

  • Linhas representam itemsets de alta utilidade encontrados.​
  • Cada linha possui 3 seções:​
    1. O itemset, com os ids ou nomes dos itens separados por espaço simples, depende da existência da 1ª parte do arquivo de entrada.​
    2. “#SUP: {VALOR}” onde {VALOR} é o suporte do itemset (nem todos os algoritmos geram esse valor)​
    3. “#UTIL: {VALOR}” onde {VALOR} é a utilidade do itemset.
Arquivo de saída

Referências