Artigo 3: Representation Learning for Frequent Subgraph Mining

A mineração de dados é uma área de estudo e pesquisa cada vez mais frequente devido ao seu impacto e capacidade de extração de informações relevantes em grandes conjuntos de dados. Nesse sentido, uma das principais subáreas de mineração de dados é a de mineração de subgrafos frequentes.

Em termos gerais, dado um grafo, essa área de pesquisa se concentra em descobrir algoritmos e heurísticas que permitem analisar quais são os subgrafos de maior importância (motif) e que ocorrem com maior frequência dentro desse mesmo grafo. Sabe-se que esse é um problema de natureza difícil, devido à alta explosão combinatória do espaço de solução. Por isso, muitos estudos são feitos para desenvolver uma abordagem eficiente de solução do problema.

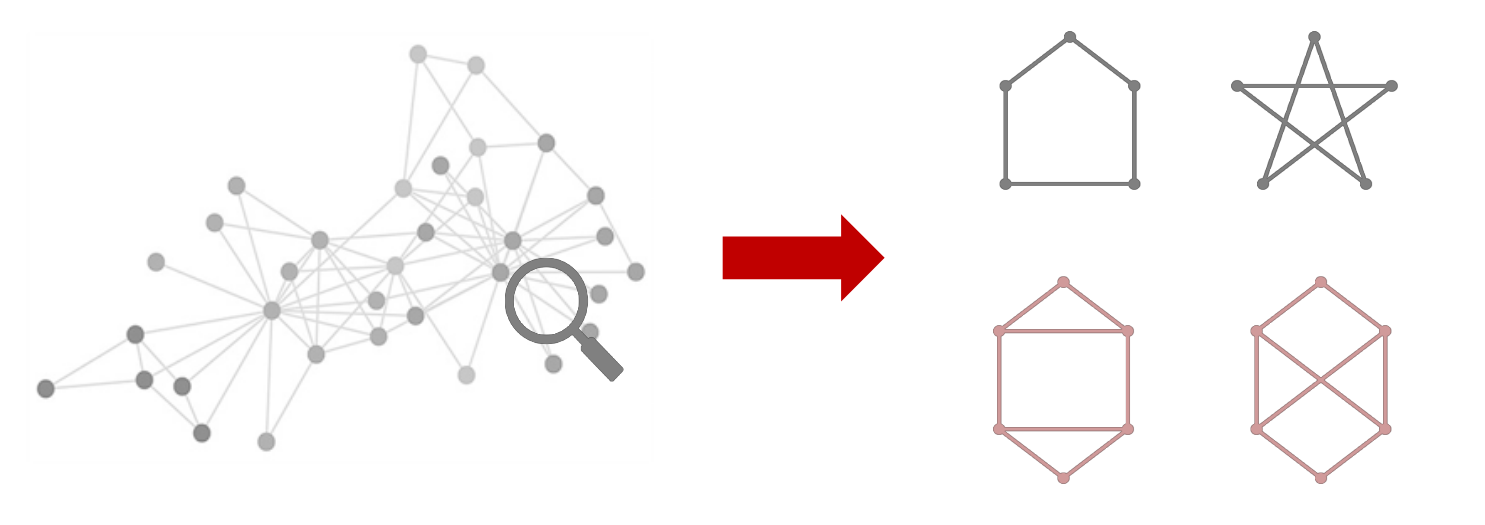
Contextualização do Problema

A motivação para desenvolver soluções nesse tipo de análise de dados é diversa. Dentre as áreas em que é possível aplicar essa técnica, podemos destacar: a biologia e a química, no estudo e pesquisa de fármacos e das relações entre átomos e ligações químicas; o setor de transporte, na análise de rotas mais eficientes e baratas para deslocamento; assim como redes de computadores, no estudo das conexões entre diferentes computadores e servidores de modo a encontrar redistribuições mais rápidas e eficientes de pacotes, entre outras.

Algoritmos Clássicos

Os algoritmos clássicos de mineração de subgrafos frequentes baseiam-se em abordagens similares àquelas usadas na mineração de conjuntos de itens frequentes. Em resumo, consistem na geração de candidatos e no crescimento de padrões para encontrar os subgrafos recorrentes na base de dados.

Tais abordagens apresentam tanto vantagens como desvantagens, dentre as quais vale destacar:

	Geração de Candidatos	Crescimento de Padrões
Vantagens	- Simples	- Redução do espaço de busca por meio de podas
	- Natural	- Eliminação de redundâncias

Desvantagens	- Explosão combinatória do número de candidatos	- Alto custo na verificação dos subgrafos
	- Extremamente ineficiente em grandes grafos	- Ineficiente em grandes grafos
	- Consome grande quantidade de recursos como memória

SPMiner: Uma abordagem inovadora

Com o problema contextualizado, fica evidente a importância da pesquisa conduzida pelos autores do artigo. A abordagem proposta por eles consiste no uso de aprendizado profundo para tornar a computação dos subgrafos frequentes eficiente. A ideia principal é utilizar uma Rede Neural em Grafos (GNN) para mapear subgrafos para um espaço ordenado de embeddings multidimensional de modo que a busca por subgrafos frequentes nesse espaço seja mais rápida.

A construção da rede neural foi feita justamente com esse objetivo, de modo que a arquitetura e a função de perda utilizada garantam que a relação de ordem parcial entre subgrafos seja mantida. Em termos gerais, se um subgrafo A é subgrafo de B, então A se encontra abaixo e à esquerda de B no espaço de embeddings citado.

O Algoritmo do SPMiner

Identificar subgrafos frequentes de importância, também chamados de Redes Funcionais (Network Motif) é crucial para analisar e prever propriedades de redes do mundo real. Contudo, encontrar grandes redes funcionais comuns é um problema desafiador não apenas devido à sua sub-rotina NP Difícil de contagem de subgrafos, mas também ao crescimento exponencial do número de possíveis padrões de subgrafos.

O algoritmo SPMiner alia o poder das seguintes áreas: redes neurais de grafos, espaços latentes ordenados (order embedding space) e uma estratégia de busca eficiente no espaço de possibilidades. Isso possibilita a identificação de padrões de subgrafos de rede que aparecem com mais frequência no grafo de destino.

Para tal, de forma simplificada e ordenada, ele segue os seguintes passos:

Decompõe o grafo de destino em subgrafos sobrepostos ancorados;
Mapeia cada subgrafo do passo anterior em um espaço multidimensional latente ordenado;
Utiliza um caminhamento monotônico no espaço resultante do passo anterior;
Identifica as Redes Funcionais frequentes.

O algoritmo não é exato, porém o tempo de execução é mais de 100 vezes menor do que os algoritmos exatos e é preciso para subgrafos pequenos. Como limitação ele não é capaz de retornar a frequência dos elementos. De uma maneira geral ele representa uma inovação na área e sua estrutura básica pode inspirar na busca de soluções para outros problemas de mesma magnitude, a exemplo dos combinatoriais.

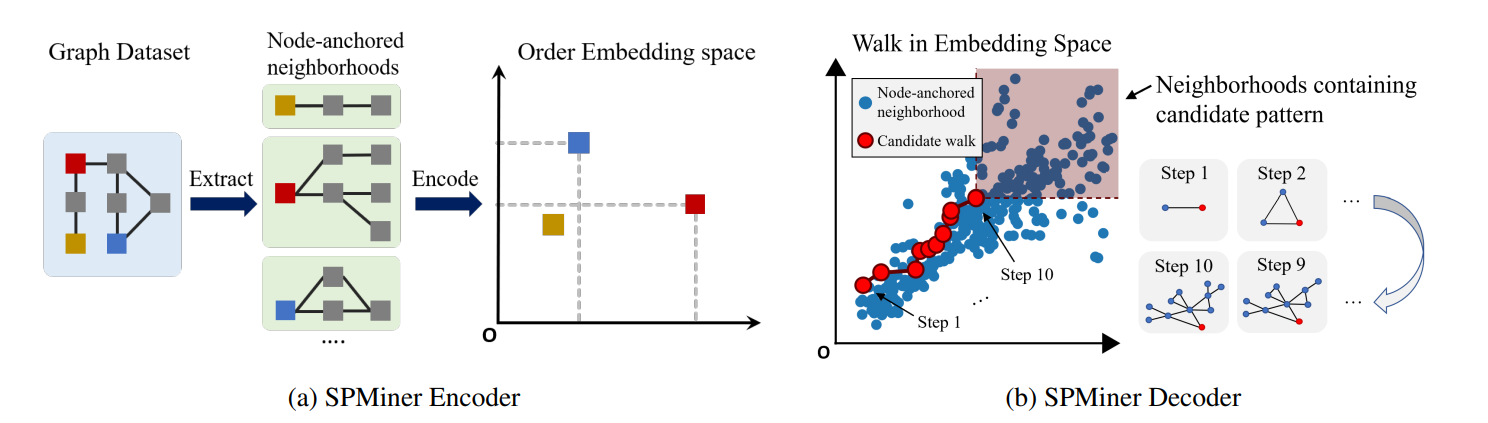
Diagrama representativo do encoder e decoder do SPMiner

Abaixo segue a descrição detalhada de cada passo.

A decomposição do grafo inicial é baseada na definição de redes funcionais ancoradas. Define-se \(G_T\) o grafo inicial, decomposto em seus vértices \(V_T\) e arestas \(E_T\) da seguinte forma \(G_T=(V_T,E_T)\). Analogamente, define-se \(G_Q=(V_Q,E_Q)\) como sendo a busca de uma rede funcional. O problema é determinar se uma cópia isomórfica de \(G_Q\) aparece em \(G_T\), ou seja, se existe uma função injetora entre os vértices e arestas de ambos.

A definição de um subgrafo ancorado é dada da seguinte forma: Seja \((G_Q, v)\) um padrão de subgrafo ancorado no vértice \(v\). A frequência do motivo \(G_Q\) no conjunto de dados do grafo \(G_T\), em relação à âncora \(v\), é o número de vértices \(u\), em \(G_T\) para o qual existe um isomorfismo de subgrafo \(f: V_Q→ V_T\) tal que \(f(v) = u\).

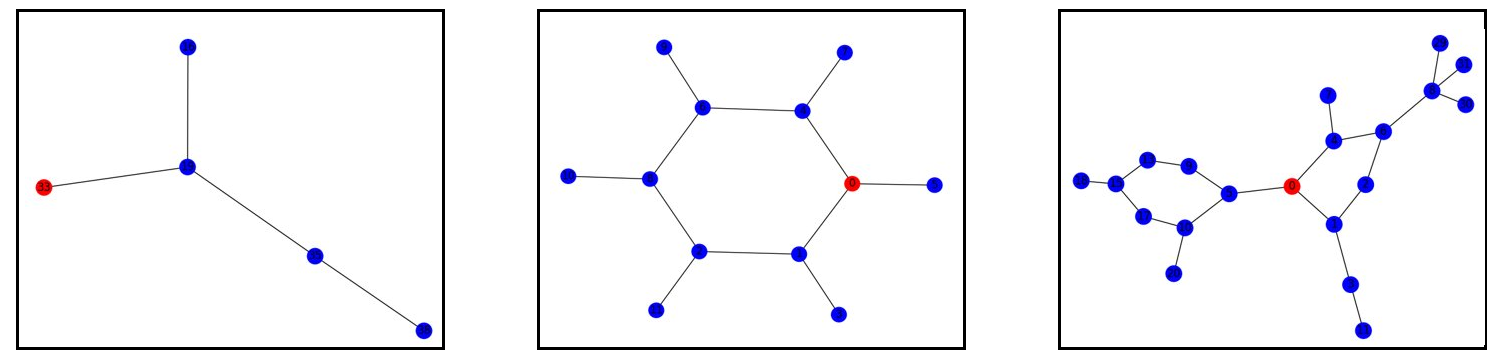
Define-se a frequência como o número de subconjuntos exclusivos de vértices \(S ⊂ V_T\) para onde existe um isomorfismo de subgrafo \(f : V_Q → V_T\) cuja imagem é \(S\). Comparado com estado da arte, esta medida é mais robusta a outliers, provê uma visão holística e satisfaz a propriedade de Downward Closure Property (DCP).

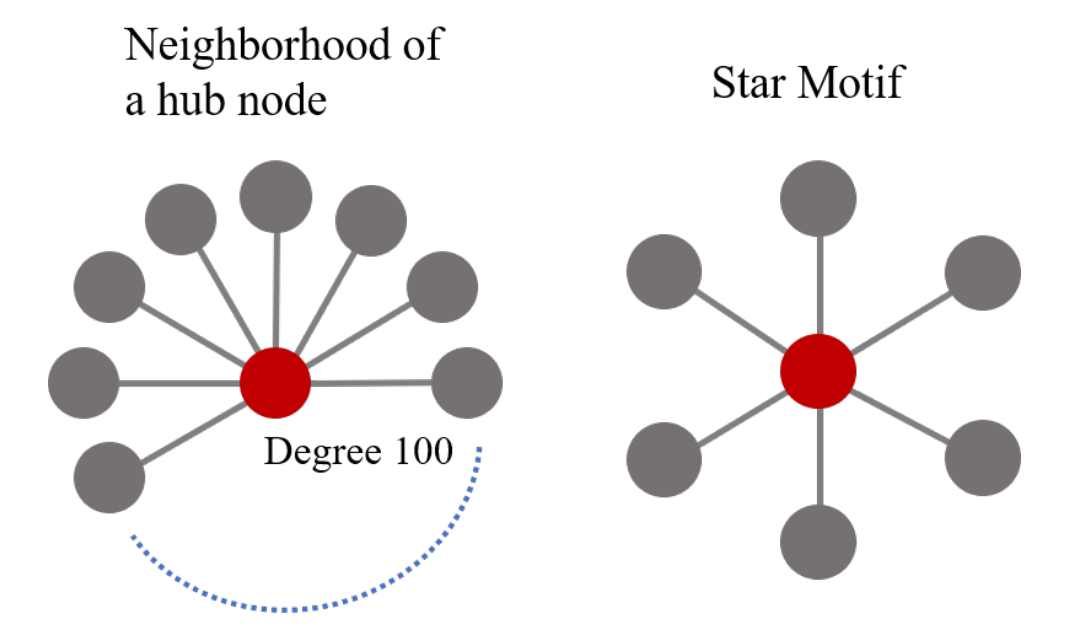
Diferença entre a frequência de subgrafos ancorados em nós e em nível de grafo.

Na imagem acima, encontram-se no grafo à esquerda uma frequência de \(\binom{100}{6}\) subgrafos isomórficos ao grafo da direita e uma medida ancorada de 1.

Portanto, dado um grafo \(G_T\), um parâmetro de tamanho de subgrafo \(K\) e o número desejado de resultados \(R\), o objetivo do SPMiner é identificar, dentre todos os possíveis grafos de \(K\) vértices, os \(R\) subgrafos com a maior frequência em \(G_T\).

Dadas as definições, a decomposição de \(G_T\) é feita extraindo os k-hop vizinhos \(G_V\) ancorada em cada vértice \(v\), ou seja, os que contém todos os vértices que têm o caminho mais curto de no máximo \(k\) para o vértice \(v\).

O processo de mapeamento para o espaço latente ordenado é feito por uma rede neural utilizando o nó âncora como uma feature categórica. O SPMiner usa essa Rede Neural de Grafo (GNN) para aprender uma função de incorporação φ, que mapeia os vizinhos ancorados em nós em pontos no espaço latente tal que a propriedade do subgrafo é preservada. É importante ressaltar que o SPMiner GNN é treinado apenas uma vez e depois pode ser aplicado a qualquer grafo de destino em qualquer domínio.

Para caminhar no espaço latente, o trabalho sugere três estratégias: a heurística gulosa, a busca em feixes e o algoritmo Monte Carlo Tree Search (MTCS). Para a estratégia gulosa, o trabalho apresenta a função de perda que será avaliada. No algoritmo de busca em feixe, concilia-se a busca em profundidade com a estratégia gulosa. Já para o algoritmo MTCS, o trabalho apresenta uma função objetivo com base no critério superior de confiança para árvores (UCT).

Dessa forma, dado o resultado da exploração do espaço, o algoritmo informa os subgrafos mais frequentes.

Metodologia Experimental

O SPMiner foi comparado com outros métodos aproximativos e, quando viável, com métodos de enumeração exata. As comparações podem ser divididas em 3 grupos: subgrafos pequenos, subgrafos grandes plantados e subgrafos grandes reais.

Para os subgrafos pequenos, a comparação com métodos de enumeração exata é possível, o que torna a comparação de desempenho mais sólida. Os subgrafos grandes plantados são subgrafos gerados artificialmente. A ideia é ter um parâmetro mais realista do desempenho na prática. A abordagem é vantajosa, pois combina grafos maiores, que são o conjunto de interesse para a aplicação, e permite avaliar o desempenho de forma mais objetiva. A última abordagem, a de comparação com grafos grandes reais, contrasta com os métodos aproximativos, mas é a que melhor aproxima o uso prático. Os datasets utilizados nessa fase incluem aplicações em diversos domínios: biologia (ENZYMES), química (COX2) e imagens (MSRC).

Também foi feita uma comparação do tempo de execução. Foram usados dois algoritmos como baseline: o MFInder (Kashtan et al., 2004) e o RAND-ESU (Wernicke, 2006). Os parâmetros foram adequados para se obter um número comparável de subgrafos e tempo de execução.

Resultados

O SPMiner tem uma acurácia significativa na identificação de motifs nos subgrafos pequenos. O SPMiner encontra motifs de tamanho 5 e 6 em até 90% das vezes. A comparação de tempo de execução é drástica: o método de enumeração ESU (Wernicke, 2006) demora cerca de 10 horas, enquanto o SPMiner executa em apenas 5 minutos. Similarmente, para os subgrafos plantados, o desempenho também foi satisfatório.

Comparação entre SPMiner e principais algoritmos aproximados de mineração de subgrafos. Os 10 principais motifs identificados pelo SPMiner têm frequência mais alta do que aqueles encontrados pelas baselines, para motifs de tamanho 5 e tamanho 6

Comparação das frequências medianas de motifs identificados por diferentes estratégias de busca e baselines.O SPMiner encontra padrões com uma frequência ancorada em nós mais alta do que as baselines MLP neural ou as baseadas em amostragem Rand-ESU e MFinder, nos conjuntos de dados COX2 (A), ENZYMES (B) e ENZYMES (C)

Frequência de motifs identificados por Gaston, gSpan, Motivo e SPMiner. O SPMiner é capaz de identificar motifs de alta frequência de grande tamanho

Comparação de tempo de execução entre métodos não neurais e o SPMiner

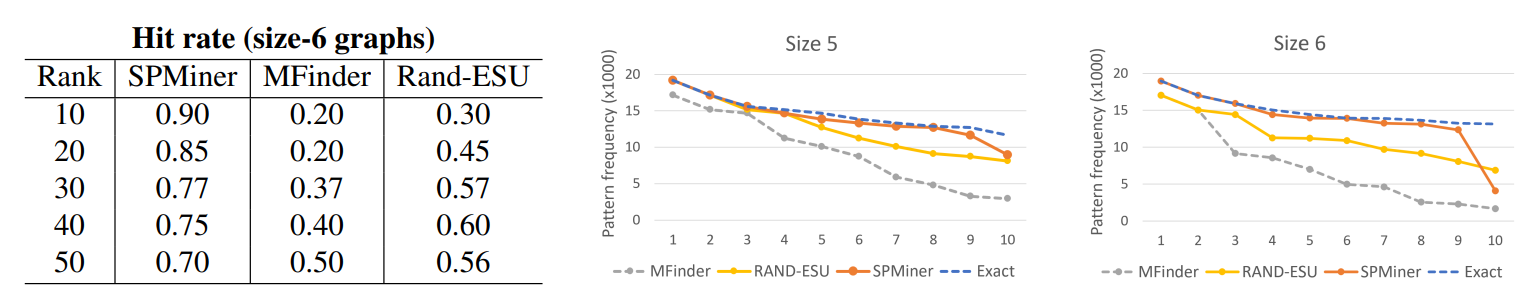
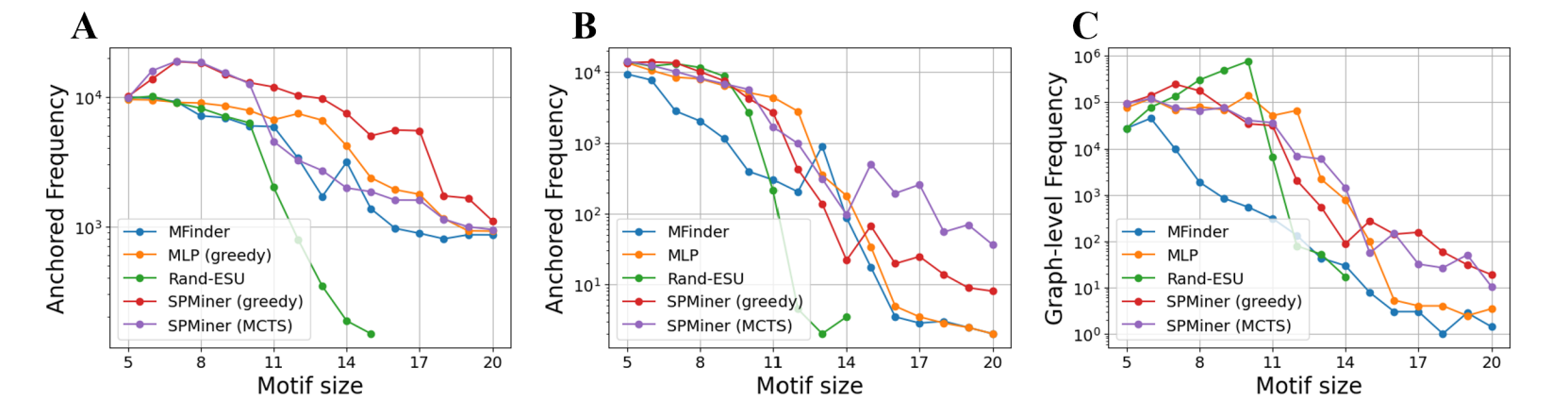
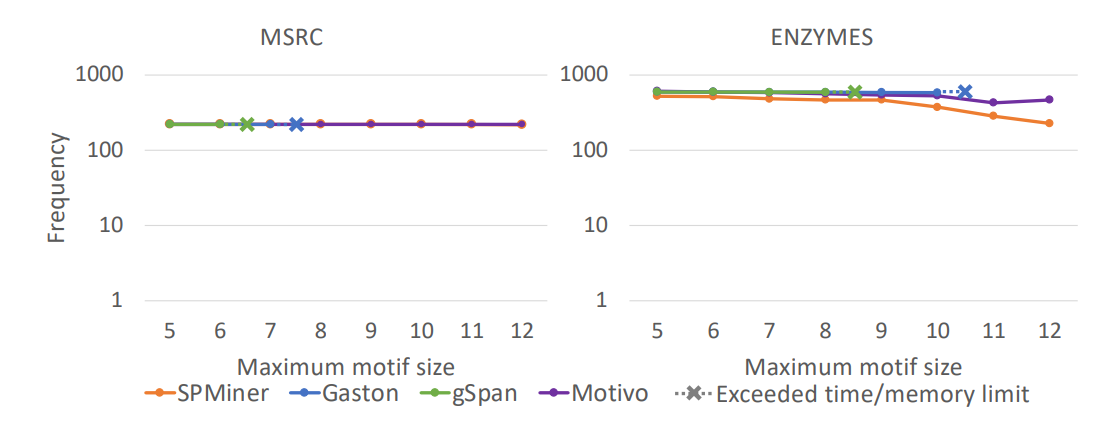
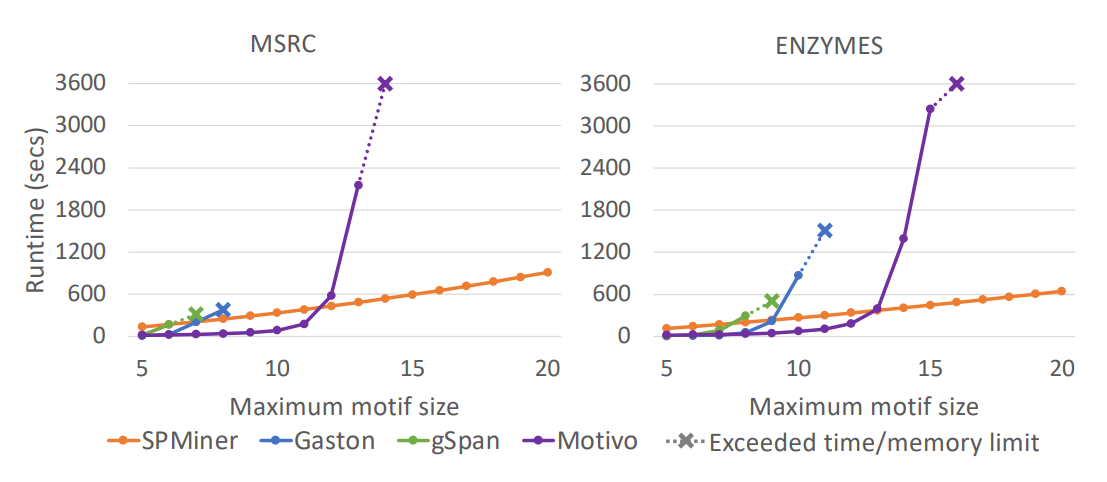
Para os subgrafos grandes reais, a identificação dos motifs foi de 10 a 100 vezes mais frequente. Além disso, o SPMiner consegue identificar motifs grandes, com 10 vértices ou mais, enquanto a mediana dos baselines é 3. Uma das vantagens do SPMiner é o pré-treinamento, que é executado apenas uma vez e é generalizável para qualquer grafo. Isso reduz drasticamente o tempo de execução, em particular se comparado aos métodos exatos.

Apesar das vantagens, o algoritmo também possui suas limitações. O treino com grafos aleatórios pode limitar sua aplicabilidade em análise de bancos de dados reais. Além disso, o algoritmo retorna apenas os k motifs mais frequentes, sem considerar a ordenação.

Aplicações e Desafios

O uso de algoritmos de recuperação de informação relacionados a subgrafos é amplamente difundido no meio industrial, acadêmico e social, tais como: 1. no meio industrial, destacam-se a indústria química e farmacêutica na produção de elementos químicos específicos e fármacos; 2. na engenharia de software, destaca-se a sua utilização no desenvolvimento de fluxos de controle de aplicações; 3. no comércio eletrônico, têm-se os sistemas de recomendação; 4. no setor bancário, atua na detecção de fraudes, 5. na cadeia de suprimentos, detecta rotas e identifica padrões logísticos; 6. no meio acadêmico, a área da bioinformática destaca-se em questões ligadas a redes de proteínas e conjuntos de proteínas; 7. na ciência ambiental, auxilia na identificação de habitats críticos para a conservação; 8. no meio social, destaca-se detecção de rotas frequentes para planejamento urbano, novos negócios e definição de rotas de fuga.

O algoritmo também possui tais desvantagens: 1. pela análise de redes sociais é possível propagar informações maliciosas, perda de privacidade e perda da autonomia individual; 2. na área comercial é possível induzir o consumo desnecessário.

Dentre os usos específicos do algoritmo, incluem-se artigos de aplicação para a detecção de rumores ou notícias falsas em redes sociais (Detecting rumours with latency guarantees using massive streaming data). E um novo algoritmo chamado Multi-SPMiner já foi proposto (Multi-SPMiner: A Deep Learning Framework for Multi-Graph Frequent Pattern Mining with Application to spatiotemporal Graphs).

Como Usar o SPMiner

Jure Leskovec, professor da Universidade Stanford e um dos autores do artigo que apresenta o SPMiner, comanda um projeto denominado Stanford Network Analysis Platform (SNAP). O projeto consiste no desenvolvimento e manutenção de um sistema de código aberto para a análise de redes complexas. Um dos módulos do SNAP, é o Neural Subgraph Learning (NSL), que consiste em uma biblioteca com várias rotinas dedicadas ao aprendizado de relações de subgrafos, e um dos algoritmos implementados é o SPMiner.

A fim de solucionar problemas de compatibilidade de bibliotecas, conflitos de instalação e facilitar a execução em ambientes diferentes, foram feitas modificações na implementação disponibilizada pelo SNAP e gerado um arquivo para a criação de um ambiente Docker. O repositório completo, que inclui um pequeno tutorial para a execução do SPMiner via Docker, pode ser acessado neste link.

Além da implementação do SPMiner, os desenvolvedores do projeto SNAP também disponibilizaram datasets que podem ser utilizados para testar o funcionamento do algoritmo, além de scripts para diferentes análises dos resultados. Experimentos locais utilizando o dataset COX2, executando o SPMiner, sem GPU, obtiveram tempo de execução próximo de 40 minutos.

Subgrafos frequentes de tamanho 5, 12 e 20, respectivamente, resultantes da mineração de padrões no dataset COX2, composto por 467 grafos. A mineração foi realizada utilizando a estratégia de pesquisa Greedy, com padrões identificados tendo tamanho mínimo de 5 e máximo de 20. O processo de mineração levou 40 minutos e 17 segundos

Dados de entrada

Há alguns datasets no repositório, mas para uma aplicação real, o usuário pode alterar o arquivo de entrada, bem como outros parâmetros: tamanho mínimo e/ou máximo dos subgrafos frequentes, estratégia de pesquisa, dentre outros.

Os dados de entrada estão no formato txt:

A representação de cada grafo é inicializada por uma linha do tipo:
t # {id do grafo}
Em seguida, n linhas, cada uma representa um vértice:
v {id do vértice} {rótulo do vértice}
E por fim, m arestas, novamente, uma por linha:
e {id do vértice de origem} {id do vértice de destino} {rótulo da aresta}

Contudo, o código aceita outras estruturações dos grafos (por exemplo, os dados do TUDataset tem um .txt com uma lista de adjacência, entre outros adicionais).

Conclusão

O SPMiner representa um avanço significativo para a mineração de subgrafos frequentes, oferecendo uma abordagem inovadora e eficiente para a identificação de padrões em dados complexos. Com seu potencial de aplicação em uma variedade de domínios, o SPMiner promete abrir novas oportunidades de pesquisa e inovação. Ao aproveitar o poder do aprendizado profundo, o SPMiner por auxiliar na revelação de padrões ocultos e oferecer insights valiosos.

Referências

Ying, R., Fu, T., Wang, A., You, J., Wang, Y., & Leskovec, J. (2024). Representation Learning for Frequent Subgraph Mining. arXiv preprint arXiv:2402.14367. https://doi.org/10.48550/arXiv.2402.14367
SIMPLEDATAMINING. Graph Pattern Mining (gSpan) - Introduction. Disponível em: https://simpledatamining.blogspot.com/2015/03/graph-pattern-mining-gspan-introduction.html. Acesso em: 19 abr. 2024.
J, Vamsi. GRAPH MINING. Disponível em: https://www.youtube.com/watch?v=KoG5lEAJmgI&t=1694s. Acesso em: 18 abr. 2024.
Rex Ying et al. Frequent Subgraph Mining by Walking in Order Embedding Space. In: INTERNATIONAL CONFERENCE ON MACHINE LEARNING, 37., 2020, Virtual. Workshop details. Disponível em: https://icml.cc/virtual/2020/7061. Acesso em: 22 abr. 2024.
Frequent Subgraph Mining by Walking in Order Embedding Space. R. Ying, A. Wang, J. You, J. Leskovec, 2020. Disponível em:https://snap.stanford.edu/frequent-subgraph-mining/
Nguyen, T.T., Huynh, T.T., Yin, H. et al. Detecting rumours with latency guarantees using massive streaming data. The VLDB Journal 32, 369–387 (2023). https://doi.org/10.1007/s00778-022-00750-4
ZEGHINA, Assaad et al. Multi-SPMiner: A Deep Learning Framework for Multi-Graph Frequent Pattern Mining with Application to spatiotemporal Graphs. Procedia Computer Science, v. 225, p. 1094-1103, 2023. ISSN 1877-0509. Disponível em: https://doi.org/10.1016/j.procs.2023.10.097. Acesso em: 22 abr. 2024.