Artigo 2: Discovering frequent parallel episodes in complex event sequences by counting distinct occurrences
A mineração de episódios é um problema similar à mineração de sequências, onde o objetivo é encontrar episódios (sequências de eventos) frequntes. Isso é feito a partir de uma sequência única com eventos temporais, com timestamp e com ou sem ordem (ou, ainda, com ordem parcial). Esse problema pode ser aplicado, por exemplo, na detecção de episódios que precedem quedas ou sobrecargas da rede elétrica.
As soluções existentes para esse problema são baseadas em gerações de episódios maximais, episódios fechados e episódios geradores. Elas lidam apenas com episódios em série e, em sua maioria, em sequências simples, onde existe apenas um episódio por timestamp.
EMDO e EMDO-P
Os autores do artigo propõem dois novos algoritmos para mineração de episódios: o EMDO (Episode Mining under Distinct Occurences) e o EMDO-P (Episode Mining under Distinct Occurences with Pruning). Eles são capazes de lidar com episódios paralelos e com sequências complexas, onde há mais de um episódio por timestamp. Além disso, uma nova definição de frequência é introduzida e utilizada por esses algoritmos. Isso foi feito pois as definições pré-existentes podem levar a uma sub ou superestimação:
Considerando o padrão xy, a imagem abaixo mostra uma definição de frequência que superestima a contagem (todas as ocorrências de x são comparadas com todas as ocorrências de y) para 4:
Já nessa imagem, temos um exemplo da subestimação para o mesmo padrão, onde são considerados apenas uma ocorrência de x e uma de y, que torna a frequêcia igual a 1:
Por fim, imagem a seguir ilustra a definição proposta, onde um evento pode ser usado no máximo uma vez, o que resulta em uma frequência igual a 2:
Conceitos Fundamentais
Para entendermos os algoritmos propostos e seu funcionamento, é essencial entender alguns conceitos:
- Evento: é um par (tipo do evento, timestamp);
- Sequência Simples de Eventos: é um conjunto ordenado de eventos, onde há apenas um evento por timestamp;
- Sequência Complexas de Eventos: é um conjunto de eventos, onde eventos podem ocorrer ao mesmo tempo;
Episódio: é um conjunto de eventos com uma relação de ordem parcial entre eles;
- Episódio Paralelo: é um episódio onde a ordem dos eventos não importa;
- Episódio Injetivo: é um episódio onde cada evento ocorre apenas uma vez.
Contagem de Ocorrências Distintas
Para evitar a superestimação ou a subestimação da frequência de eventos, a solução proposta faz a contagem das ocorrências distintas. Dessa forma, um vetor de timestamps em cada evento é utilizado para encontrar a ocorrência de episódios, e o algoritmo encontra o maior conjunto possível e ocorrências distintas.
Para um episódio ser considerado frequente, seu suporte deve ser maior ou igual ao suporte mínimo definido. O suporte do episódio é calculado pelo tamanho do seu conjunto maximal de ocorrências distintas.
Na figura a seguir, considerando o episódio xyz, temos o conjunto de ocorrências maximais distintas {[1 2 2], [1 5 4], [6 6 6]}, o que resulta em um suporte igual a 3.
Regras de Episódios
As regras de episódios são relações do tipo α ⇒ β, que representam que se o episódio α ocorreu, há grandes chances que β ocorra. Essa chance é a representação de uma probabilidade, que vem da confiança da regra, que mede a sua força. Se a confiança for maior que um limite pré-definido, a regra é válida.
EMDO
O EMDO é o primeiro algoritmo proposto no artigo, que tem como objetivo achar episódios frequentes. Para isso, ele primeiro encontra todos os episódios de tamanho 1 que são frequentes. Em seguida, esses episódios são combinados para gerar candidatos maiores e o suporte (ocorrências distintas) desses novos episódios é calculado. Além disso, para melhorar o desempenho do algoritmo, a poda dos episódios infrequentes é realizada com base na propriedade da anti-monotonicidade, diminuindo o espaço de busca.
Propriedade da Anti-monotonicidade
A propriedade da Anti-monotonicidade afirma que, sendo α e β dois episódios de forma que α está contido em β, se o episódio β é frequente então α também é frequente. Da mesma forma, se α é infrequente β também é infrequente.
EMDO-P
O algoritmo EMDO-P é o segundo algoritmo proposto pelo artigo, e tem como objetivo encontrar as regras de episódios válidas. Primeiramente, ele executa o EMDO para gerar os episódios frequentes. Em seguida, faz o teste, para um par α e β de episódios frequentes, se a regra α ⇒ β é válida. Utiliza, em seguida, a propriedade da anti-monotonicidade para realizar a poda (pruning) dos ramos infrequentes.
Experimentos
O problema proposto é descobrir padrões frequentes em sequências de eventos complexos que acontecem no mesmo timestamp. Os experimentos tem como objetivo avaliar a eficiência e a qualidade dos padrões gerados algoritmos propostos.
Para isso, foram gerados dados sintéticos com variadas quantidades de sequências, tipos de eventos e timestamps. Os experimentos foram separados em análise de descoberta de episódios frequentes (com o algoritmo EMDO) e a descoberta de regras de episódios (com o algoritmo EMDO-P).
Resultados
As análises referentes ao EMDO foram focadas na influência do limite do suporte no número de episódios frequentes e tamanho em dados reais e sintéticos. A conclusão é que a poda com base na propriedade da anti-monotonicidade é muito efetiva em melhorar o tamanho do espaço de busca (e, consequentemente, o custo computacional).
Em relação ao EMDO-P, ele tem um custo razoável, apesar de gastar mais memória. Além disso, ele é mais rápido, pois elimina os episódios irrelevantes.
Comparação
Esse problema exato não é abordado em outros artigos, o que dificulta a comparação de resultados. Ainda assim, foi feita a comparação com algoritmos que trabalham com contextos diferentes, mas que conseguem encontrar os padrões. O EMDO foi o algoritmo que gerou menos candidatos e com padrões de regras mais ricas. Além disso, ele é o primeiro algoritmo que encontra padrões paralelos em sequências complexas, e encontra padrões não retornados por outros algoritmos.
Aplicações e Desafios
Algumas das possíveis aplicações para esses algortimos são:
- Análise de Sistemas: Diversos sistemas modernos (como redes de computadores, de dispositivos IoT) podem aplicar a descoberta de padrões para otimizar seu funcionamento;
- Análise de Comportamento: Logs de sistemas web, que são compostos de sequências de eventos complexas, podem ser analisados para otimizar a experência do usuário;
- Análise de Varejo e Comportamento de Compra: A extração de regras pode ser utilizada para desenvolver estratégias de marketing baseadas em promoções ou recomendações.
Porém, seu uso vem acompanhado de alguns desafios, principalmente quando se trata de análise de comportamento:
Vigilância e Privacidade: Com a disponibilidade de dados granulares e carimbados por timestamp, a possibilidade de rastreamento de atividades com más intenções é alta;
- Um exemplo é a vigilância de funcionários para aplicar punições;
Reforço de Viés: Ao aprender com dados históricos, que podem refletir preconceitos e desigualdades, o algoritmo reconhece esses padrões como “regras”;
Acesso à Oportunidade: Criação de sistemas de pontuação para governar acesso a serviços essenciais:
- Empresas de planos de saúde podem utilizar os dados para negar serviço ou cobrar mais de alguns clientes
De maneira geral, os algoritmos de descoberta de episódios paralelos frequentes têm diversas aplicações para melhorar os serviços, mas também um grande potencial para afetar, direta ou indiretamente, os usuários.
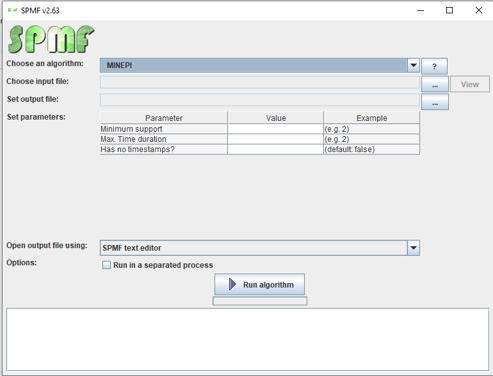
Execução
Para a execução do algoritmo, cada id dos datasets são considerados como um timestamp. Dessa forma, cada timestamp possui o conjunto de eventos. Os dados sintéticos são disponibilizados em um repositório no github, junto com a base de dados completa de algoritmos SPMF. Ela dsponibiliza diversos algoritmos, e a implementação está em Java (para qual o único pré-requisito é o jdx - java development kit). No arquivo .jar é possível escolher um algoritmo para rodar. No entanto, os algoritmos propostos no artigo não estão incluídos nesse repositório, e, após uma busca detalhada, não foi possível localizar suas implementações disponíveis publicamente online. Isso limitou a possibilidade de comparação direta com os métodos existentes na SPMF.
Conclusão
O problema indicado no artigo, apesar de ser apresentado como algo inédito, é muito semelhante à mineração de padrões, se o timestamp for desconsiderado. Ao utilizar a definição de episódio paralelo, qualquer item em uma transação pode ser utilizado na contagem. Assim, os algoritmos EMDO e EMDO-P, apesar de mostrarem um bom funcionamento, não apresentam uma grande motivação para o seu uso. Além disso, a falta de disponibilidade do código fonte e diversos erros como falhas textuais, definições mal formadas e imagens incompletas comprometem reprodutibilidade dos experimentos e a compreensão dos resultados. Dessa forma, embora o artigo traga contribuições interessantes, ele peca na falta de uma fundamentação mais sólida e de uma apresentação mais cuidadosa para justificar a relevância dos algoritmos propostos.
Referências
- Ouarem, O., Nouioua, F. & Fournier-Viger, P. Discovering frequent parallel episodes in complex event sequences by counting distinct occurrences. Appl Intell 54, 701–721 (2024). https://doi.org/10.1007/s10489-023-05187-y